WeeklyStudy

Posted on 2023-12-31 Edited on 2024-12-05 In Description Symbols count in article: 96k Reading time ≈ 1:27

2023摸鱼笔记哈哈哈哈。

230201

dp泄露以及一些扩展

n, e, dp, c

即基础$dp$，需要进行一定推导，主要以推导＋爆破的思想，对n进行分解，从而得到$p$, $q$。

变种1：$n = p^{b} \cdot q$

def dp_hensel(c, e, dp, p, b):
    """
    :param b: p^b*q
    :return:
    """
    mp_ = pow(c, dp, p)
    mp = pow(c, dp - 1, p)
    for i in range(1, b - 2):
        x = pow(c - pow(mp_, e), 1, p**(i + 1))
        y = pow(x * mp * invert(e, p), 1, p**(i + 1))
        mp_ = mp_ + y
    return mp_

[2020YCB]Power

关于十进制位数与二进制位数。

感觉十进制的不会太容易比较，还是直接比较二进制的相对来说会比较准确一点。二进制的话主要利用bit_length()函数。
$$
d\times e \equiv 1 \mod phi \equiv 1\mod (p-1)
$$

$$
dp \equiv d \mod (p-1)
$$

$$
k \times ( p - 1 ) = dp \times e - 1
$$

# num = dp * e - 1
# num.bit_length() 为 526
# yafu对num进行分解，从而得到因子
"""
factor:
P1 = 2 # 1 digits
P1 = 2
P1 = 2
P2 = 11 # 2
P4 = 7411 # 4
P14 = 10402958442703 # 14
P17 = 25388174482857437 # 17
P23 = 19976951634728916570101 # 23
P33 = 121098273308863403811867260913043 # 33
P69 = 514664028984426592785192432611128951474323755859087258008037664208623 # 69
"""
# 利用范围框定p值，经过试验得：
p = num // 7411 // 2 // 2 + 1
# print(p.bit_length())
# 512
# 判定条件
# 1. 数值长度是否512
# 2. 所得p是不是素数

主要利用分解出来的factors，来进行试错，然后通过查看bit位数的函数，唯一的p给试出来。
$$
c \equiv m^{e} \mod n
$$

$$
dp \equiv d (\mod p-1)
$$

$$
\rightarrow c^{dp} \equiv m^{e\cdot dp} \mod n
$$

$$
\rightarrow c^{dp} \mod p \equiv m^{e \cdot dp} \mod p
$$

$$
d\cdot e \equiv 1 \mod lcm(p-1, q-1)
$$

$$
\rightarrow e\cdot dp \equiv d \cdot e \mod (p-1) \equiv 1 \mod (p-1)
$$

$$
\rightarrow k\cdot (p-1) = e \cdot dp - 1
$$

$$
\exist k \in \mathbb{Z}, c^{dp}\mod p = m^{k\cdot (p-1) + 1} \mod p
$$

费马定理可得$a^{p-1} \mod p \equiv 1$.
$$
\Longrightarrow m \cdot m^{k\cdot (p-1)} \mod p \equiv c^{dp} \mod p
$$

$$
\Longrightarrow m \equiv c^{dp} \mod p
$$

"""
Hensel lifting for Takagi’s scheme
"""
dp = 3272293505696712831419859641571956066667516012597886098021642320155056349966612629986261146617139998624603483170466852538289743936225789351270153550594329
c = 22524257534087703614496632403022329621384173069680778965750290698059674588465640878754707363673789674111671270645152584118206145007310499274423606886261969807360070526126452646719628307689968971699215841867636770320159256301550908771135042912287955209485328267670825390080110910391913063177323585204392804538642393453388536211144485389902591029350060800993352969569703901717308330574394200996651534321547814313195218895547718815009876393987398738932001924661338796059973950012706427109598830049455186171345179840564502215531573714428772608739268313985559628612004439028014417408631851880698512023740903181116906766066951473942201698375224240271523568161242951730224901227589413731025281719101368668617497947995579443908773425555177346524678673641140157885033923288401884
c1 = 290707924192892686920253390955676600323331633814839708838347288502692494699485764473635783441705302268064111648851157070038783719749721994682837294625334517914882191486257362565066745587415388291939979195637720350919055988532145531805200483161599965215275808797976727969023747299578173497083532351976473770041800769265319548352841139802163279116490053292316399038329210043455932786945180855178341998049756983301499491011851026499269682821602212971062877270127451987836730083380463825717889123804613394241190839837791281657872259492589868751745327696030438893865069941066073554427558697972551085353027574529823439588670263047287131740802375738439636789806332323994866753085014446479034974063195632514803340511247735647970572837053148490258113394359072976858781060349776921428492973183958437965966963122069107876143476772436757554253049619918403996315720023020827394900507088006299225934263699192253079026440287311664705744424959801981503191480257138833694306501816837037995549817186335377411638035575004595417788588264823861850877111374085336446477943372458378834664678094751978400910288151519902977326995118727880223621964441498323865158898463327323193833062919619201107279964663654606753750042791368210261574897455830722232022689695292080269205470491791950839486861811469879413313773338916781857981641910031441448964144000585506870170898052132929034349451945051362244755750988705018897859238859476967568556992146975789444151432386692872801263000639711599152191790766776280
y = 449703347709287328982446812318870158230369688625894307953604074502413258045265502496365998383562119915565080518077360839705004058211784369656486678307007348691991136610142919372779782779111507129101110674559235388392082113417306002050124215904803026894400155194275424834577942500150410440057660679460918645357376095613079720172148302097893734034788458122333816759162605888879531594217661921547293164281934920669935417080156833072528358511807757748554348615957977663784762124746554638152693469580761002437793837094101338408017407251986116589240523625340964025531357446706263871843489143068620501020284421781243879675292060268876353250854369189182926055204229002568224846436918153245720514450234433170717311083868591477186061896282790880850797471658321324127334704438430354844770131980049668516350774939625369909869906362174015628078258039638111064842324979997867746404806457329528690722757322373158670827203350590809390932986616805533168714686834174965211242863201076482127152571774960580915318022303418111346406295217571564155573765371519749325922145875128395909112254242027512400564855444101325427710643212690768272048881411988830011985059218048684311349415764441760364762942692722834850287985399559042457470942580456516395188637916303814055777357738894264037988945951468416861647204658893837753361851667573185920779272635885127149348845064478121843462789367112698673780005436144393573832498203659056909233757206537514290993810628872250841862059672570704733990716282248839
g = 2
e = 0x10001
b = 4
"""
p解法1
"""
from gmpy2 import *
# num = e * dp - 1
# p = (e * dp - 1) // 7411 // 2 // 2 + 1
# # print(p.bit_length())
# # print(is_prime(p))

# from sympy import *
"""
p解法2
"""
# x = discrete_log(y, c1, 2)
# print(x)
# print(type(x))
# print(type(y))
x = 5535722692962580764045545539105119140941061679289569420988353884209653851308860058948669740693107863231179565602072744542122031789184119031739723962825082929025825322421201364211726001366490949760887367407718763255964735567971493859197583624076478457865073449246835949075135223468616834636386958924709024763349115622062848212445867198457630368236782421195503713107838541903829979118327675371550868768159024260793541264335548489228744367609071659968450303895118817379316060805148754136917043160175570565717388336822960389664337656603584425629662613786203920234401824957121860225422901340950436355650311392398098947210940
p = var('p')
R.<p> = PolynomialRing(GF(y))
# R = PolynomialRing(GF(y), name = 'p')
f = 2019*p**2 + 2020*p**3 + 2021*p**4 - x
# print(f)
f.roots()

"""
p解法3
"""
for x in range(1,e+1):
    if (dp*e-1)%x==0:
        p=(dp*e-1)//x+1
        x = 2019*p**2 + 2020*p**3 + 2021*p**4
        if c1 == pow(g, x, y):
            print(p)
            break

def dp_hensel(c, e, dp, p, b):
    """
    :param b: p^b*q
    :return:
    """
    mp_ = pow(c, dp, p)
    mp = pow(c, dp - 1, p)
    for i in range(1, b - 2):
        x = pow(c - pow(mp_, e), 1, p**(i + 1))
        y = pow(x * mp * invert(e, p), 1, p**(i + 1))
        mp_ = mp_ + y
    return mp_

"""
解法2：根据Hensel lifting for Takagi’s scheme算法进行解密
"""
from Crypto.Util.number import long_to_bytes
m = int(dp_hensel(c, e, dp, p, b))
print(m)
print(long_to_bytes(m))

# """
# 解法1：利用推导定位关键公式进行解密
# """
# # m = pow(c, dp, p)
# # print(m)
# # print(long_to_bytes(m))

变种2：Coppersmith攻击，已知dp高位攻击

#Sage
dp0 = 
e = 
n = 

F.<x> = PolynomialRing(Zmod(n))
d = inverse_mod(e, n)
for k in range(1, e):
	f = (secret << 200) + x + (k - 1) * d # 200 editable
	x0 = f.small_roots(X=2 ** (200 + 1), beta=0.44, epsilon=1/32)
	if len(x0) != 0:
		dp = x0[0] + (secret << 200)
		for i in range(2, e):
			p = (e * Integer(dp) - 1 + i) // i
			if n % p == 0:
				break
		if p < 0:
			continue
		else:
			print('k = ',k)
			print('p = ',p)
			print('dp = ',dp)
			break

变种3：$p = gcd(m^{e \cdot dp} - m, n)$

TBC

还有很多变种，暂且不明白原理，先放着了。

sagemath-preparse

体现参数调用过程，虽然代码还没出来。

question

无法理解，为啥这种定义能够报错，这出现啥问题了吗？

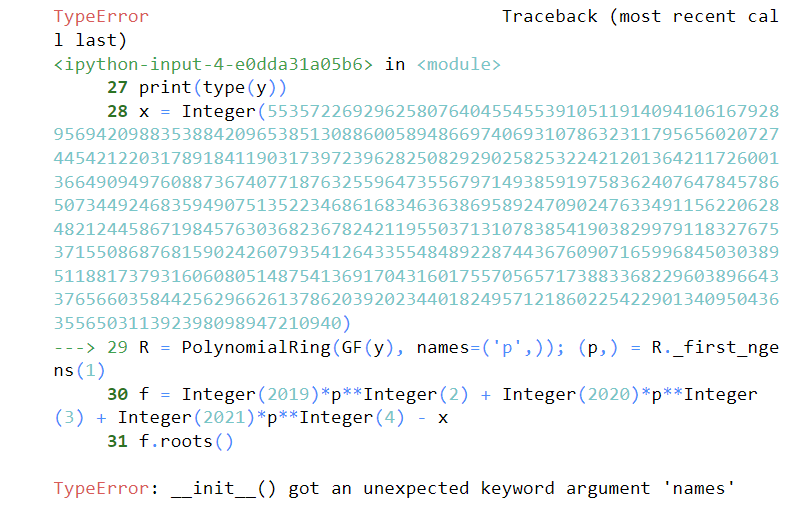
……没搞懂，先放弃了。

疑似可解：

# original: R.<x> = PolynomialRing(GF(y))
# 1
R.<x> = PolynomialRing(Zmod(y))

# 2
R.<x> = GF(y)[]

# failed

# success
p = var('p')
R.<p> = PolynomialRing(GF(y)) # 定义p为GF(y)环上的多项式未知变量

0203，不会整，不搞了。

0208，会整了，先定义。

230202

版本选择

MinGW 各版本参数说明
MinGW 可以适应不同系统开发环境，因此有几大参数需要进行选择： Version、Architecture、Threads、Exception

Version：指的是你选择的 GCC 编译器的版本，我选择的是当前最新版本 8.1.0，一般建议选择最新的版本；
Architecture：指的是你的电脑的系统类型，i686 表示的是 32 位的系统类型，x86_64 表示的是 64 位的系统类型；
Threads：指的是线程模型，posix 或 win32
- POSIX（Portable Operating System Interface，可移植操作系统接口），是 UNIX 系统的一个 API 设计标准，很多类 UNIX 系统也在支持兼容这个标准，如 Linux 操作系统。如果在 Windows 下开发 Linux 应用程序，则选择 posix；
- Win32，是 Windows 系统下一个 API 设计标准，如果开发 Windows 平台下的应用程序，就需要选择 Win32；
Exception：指的是异常处理模型。i686 系统架构有两种选择：dwarf 和 sjlj；x86_64 系统架构也有两种选择：seh 和 sjlj。
- sjlj，seh，dwarf 三者的区别：在C++中有 try…throw…catch，当它执行这种结构时，它需要保存现场还原现场，而 sjlj，seh，dwarf 正是实现这类过程的三种方式。
- sjlj 全称是 SetJump / LongJump，前者设还原点，后者跳到还原点。可用于 32 位或者 64 位系统。
- seh（Structured Exception Handling，结构化异常处理）是 Borland 公司的，微软买了其专利使用权，它利用了 FS 段寄存器，将还原点压入栈，收到异常时再弹出。相较而言，sjlj 是 C 标准库就有的东西，seh 在 2014 年前是有专利的，从性能上说 seh 比 sjlj 快。只用于64位系统。
- dwarf 只支持32位系统 – 没有永久的运行时间开销 – 需要整个调用堆栈被启用，这意味着exception不能被抛出，例如Windows系统DLL。
综上所述：
- 【x86_64 64位】
  1. seh 是新发明的，而 sjlj 则是古老的。只用于64位系统。
  2. seh 性能比较好，但不支持 32位。 sjlj 稳定性好，支持 32位和64位。
  3. 因此，x86_64 系统架构的推荐使用 seh 的异常处理模型。
- 【i686 32位】
  1. dwarf 只支持 32 位，而 sjlj 支持 32 位或64 位，但是 dwarf 的性能要优于 sjlj。
  2. 因此，i686 系统架构的推荐使用 dwarf 的异常处理模型。

<https: wiki.qt.io=”” mingw-64-bit=””

安装mingw

笑死，一直下载错了。应该是这里的压缩包，之前下载的压缩包一直是源码，难怪找不到bin目录。

MinGW-w64 - for 32 and 64 bit Windows - Browse Files at SourceForge.net

找到bin目录，并且放入环境变量后，直接运行gcc -v，让它自己自动安装。

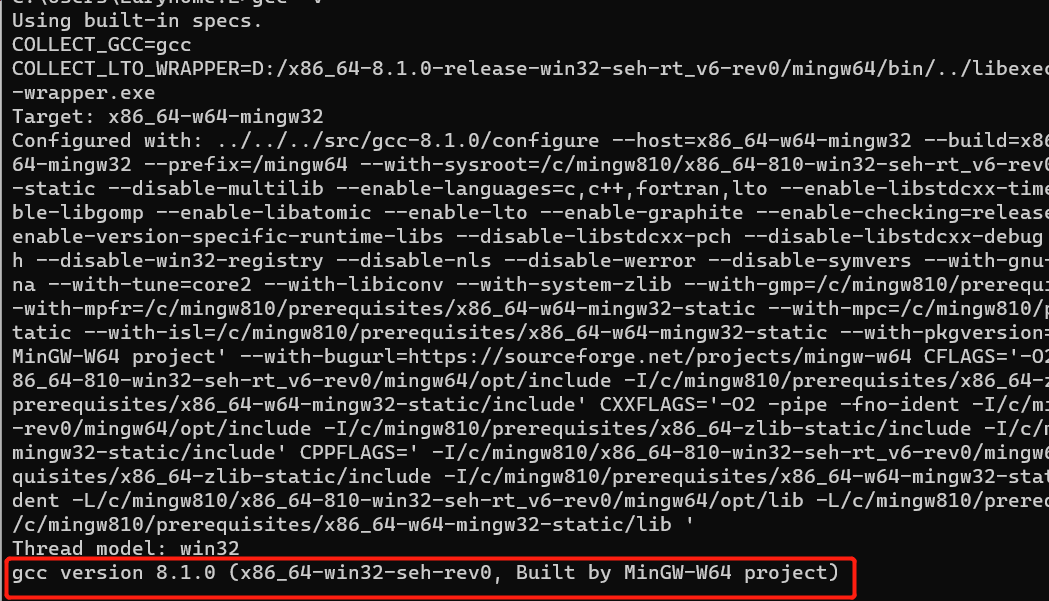
安装成功之后就是出现这下面最后一行。

把mingw导入VScode中

关键几个文件具体配置不太理解具体作用。

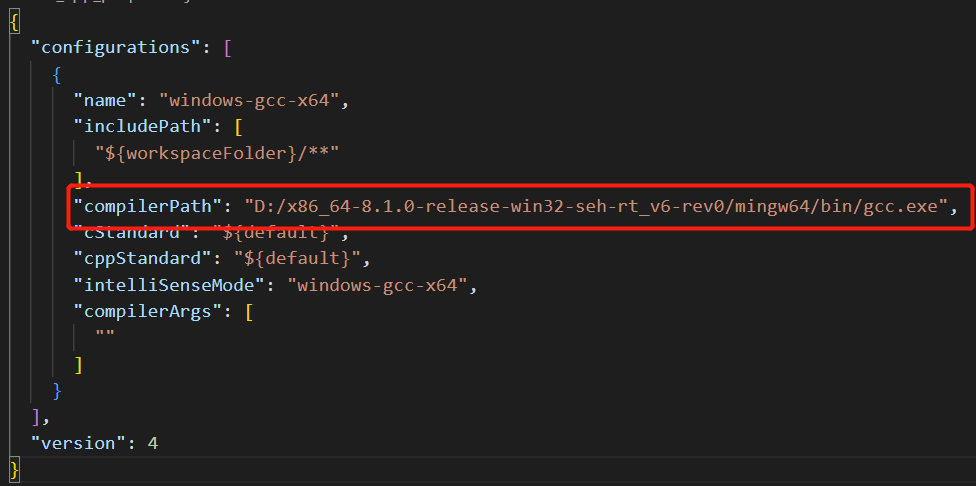
c_cpp_properties.json，运行应该是自动检测相关路径然后进行导入。

task.json用来做编译。

launch.json执行编译好的文件。

详解Linux下使用vscode编译运行和调试C/C++ - 知乎 (zhihu.com)

create task.json

选择 Terminal>Configure Default Build Task ，将出现一个下拉菜单，显示 C++ 编译器的各种预定义编译任务。选择 C/C++: g++ build active file。

# task.json
{
	"version": "2.0.0",
	"tasks": [
		{
			"type": "cppbuild",
			"label": "C/C++: g++.exe build active file",
			"command": "D:\\x86_64-8.1.0-release-win32-seh-rt_v6-rev0\\mingw64\\bin\\g++.exe",
			"args": [
				"-fdiagnostics-color=always",
				"-g",
				"${file}",
				"-o",
				"${fileDirname}\\${fileBasenameNoExtension}.exe"
			],
			"options": {
				"cwd": "${fileDirname}"
			},
			"problemMatcher": [
				"$gcc"
			],
			"group": {
				"kind": "build",
				"isDefault": true
			},
			"detail": "compiler: D:\\x86_64-8.1.0-release-win32-seh-rt_v6-rev0\\mingw64\\bin\\g++.exe"
		}
	]
}

command: 要运行的程序，此处是g++。

args： args 数组包含将传递给 g++ 的命令行参数（必须按照编译器预期的顺序指定）。${file}表示当前打开的待编译的活动文件，对它进行编译，并在当前路径${fileDirname}生成与活动文件同名无后缀的可执行文件${fileDirname}/${fileBasenameNoExtension}。在本案例中活动文件指helloworld.cpp,所生成的可执行文件为helloworld。

label: 标签值是将在任务列表中看到的内容；可以随意命名它。

group中的isDefault: 值为true表示支持通过快捷键ctrl+shift+B来执行该编译任务。如果值改为false，也可以从菜单中选择运行：Terminal>Run Build Task。

插一句：我去，我是真的都把C语言的相关给整忘了，我都压根没有先编译，我的天。

run task.json

执行tasks.json中定义的编译任务。快捷键ctrl+shift+B或者从菜单中选择运行：Terminal>Run Build Task。

应该这个才是成功吧，瘫。之前的可能端口确实被占用了。

【VSCode】解决“终端将被任务重用，按任意键关闭”问题 - 知乎 (zhihu.com)

然后新开一个terminal窗口，进入

create launch.json

launch.json文件用于在 Visual Studio Code 中配置调试器。接下来将创建launch.json 文件。

选择 **Run > Add Configuration…，选择C++ (GDB/LLDB)**。之后将看到展示各种预定义调试配置的下拉列表，选择 g++ build and debug active file。将自动生成launch.json文件。

但我没找到。

虽然没找到，但莫名其妙能运行了。

小结

调试逻辑有点让人摸不着头脑。

但能运行就暂且先不整啥东西。

230203

变种2/3，放230201了。

230206

关于如何运行已上传dockerhub中的环境

(10条消息) (三) Docker常用命令_docker run 进入已命名的容器_小怪吖的博客-CSDN博客

拉取镜像

进入超级管理模式。

docker pull dockerhub账号/dockerhub仓库名称:dockerhub标签名

以GitHub - CTF-Archives/2022-xhlj-crypto-lockbylock: A crypto challenge in 2022 西湖论剑大赛该题上传环境为例。

docker pull randark/2022-xhlj-crypto-lockbylock:master

拉取成功

docker images

查看拉取后的镜像。拉取成功。

运行拉取的镜像

docker run -tid -p xxxx:80 imageid
docker run -tid -P xxxx:80 imageid

……没成功，咋回事。

好像是成功的，但我以为没成功。

docker run -it repository:tag

停滞其中。

docker run -it -d --name name -p port:port -v path:path -v file:file -e env=value image:tag /bin/bash

似乎是完整命令。

查看运行中的程序

docker ps

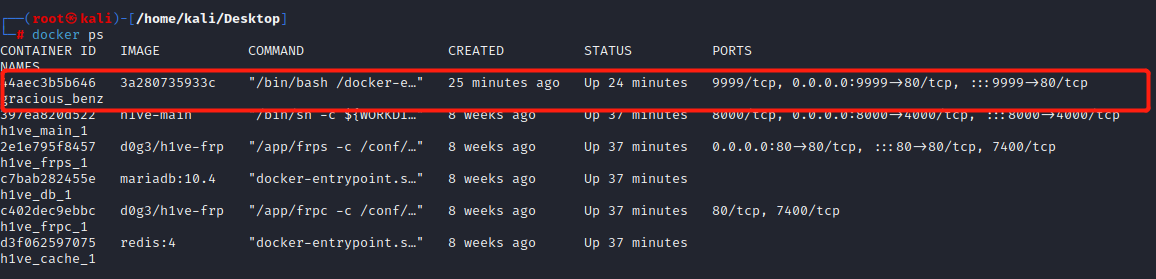
还没法用nc连接，迷茫中。

sagemath中文文档以及图形化等功能

[绘图 Lainme’s Blog]

压缩包炸弹(Zipbomb)

大压缩文件，占据大量内存。

利用脚本对大压缩文件进行检索

import os.path
import zipfile
import re

dir_path='xxx'
files= os.listdir(dir_path)
newfiles = ["zipboom.zip"]
print(newfiles)
setee = []
for file in newfiles: #遍历文件夹
    position = dir_path+'\\'+ file #构造绝对路径，"\\"，其中一个'\'为转义符
    print (position)
    z = zipfile.ZipFile(position, 'r')
    for filename in z.namelist():
        bytes = z.read(filename)
        if b'NSSCTF{' in bytes:
            print(filename)

运行后得到大压缩文件内含AAAA文件。

提取内含文件的小压缩包

利用winhex或010editor进行提取，提取完直接解压即可。

简单直接的方法

winrar直接就检索到有效文件AAAA，直接解压就可以了。

re-easyre

exeinfo查看是否加壳

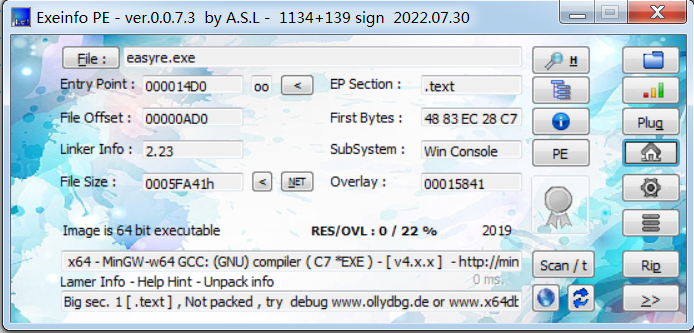
得到关键信息：

64位程序
not packed即未加壳

放入ida-64进行分析

找到main函数的入口，我在这里的话是先看exports模块中的进行查看。

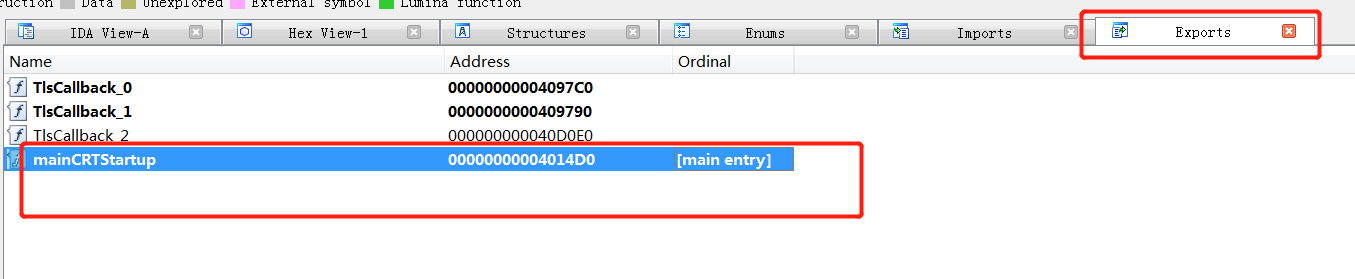
找到具体位置后，稍微查看一下就直接找到flag了。

【定位之后发现应该就是把程序拖入ida之后直接跳转到的界面。

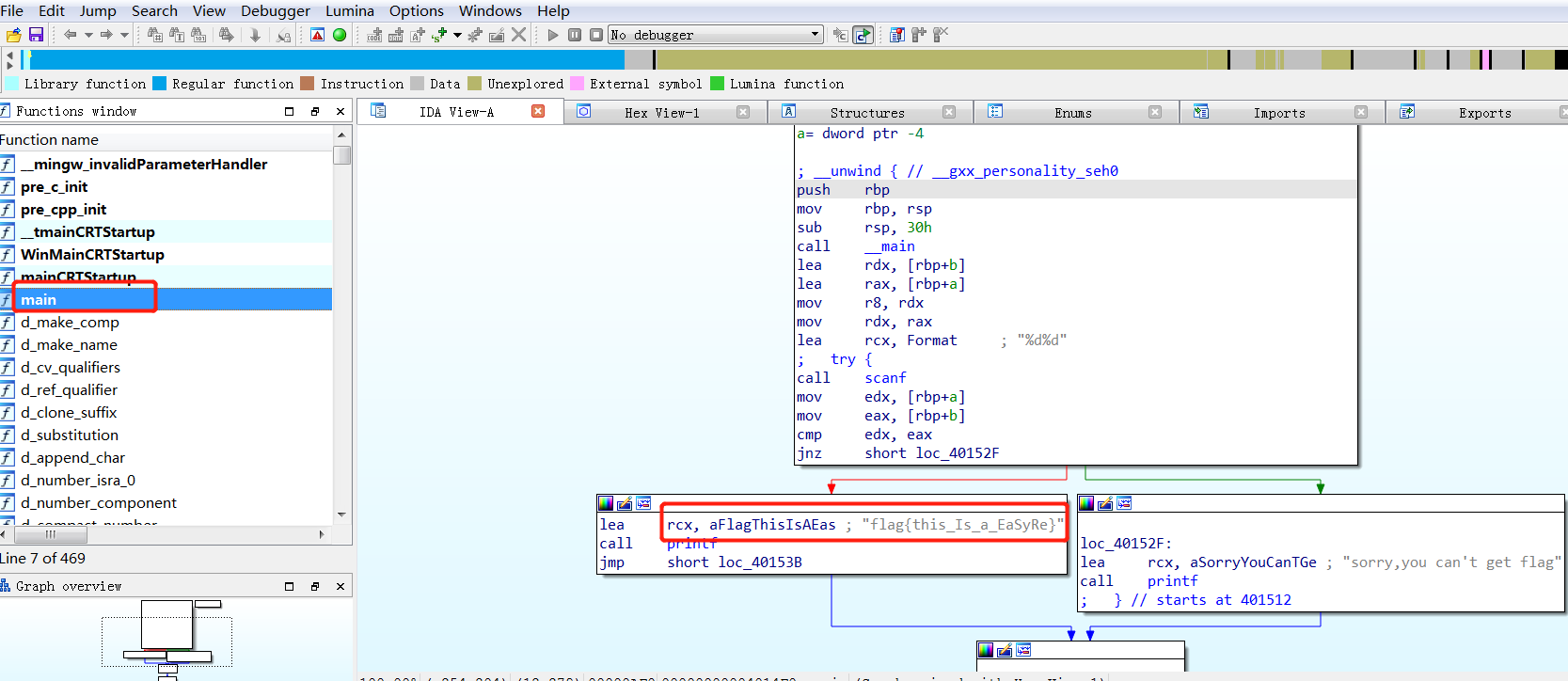
re-reverse1

前面一样的步骤。

得到信息：

64位程序文件
未加壳

先查看string窗口，发现疑似flag，进行跳转。

跳转完需要进行分析，分析完发现直接提交flag{hello_world}是错误的。

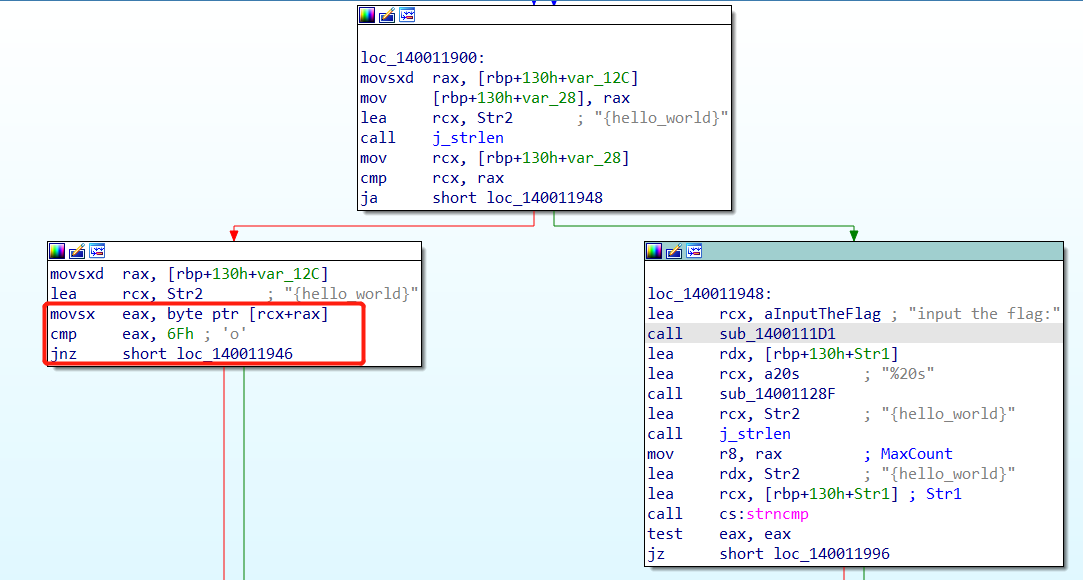
继续当前代码段进行分析，发现对字符进行了一些处理。

IDA的学习使用

图形界面/流程图界面

Yes边的箭头（是的，执行分支）默认为绿色，No边的箭头（不，不执行分支）默认为红色。

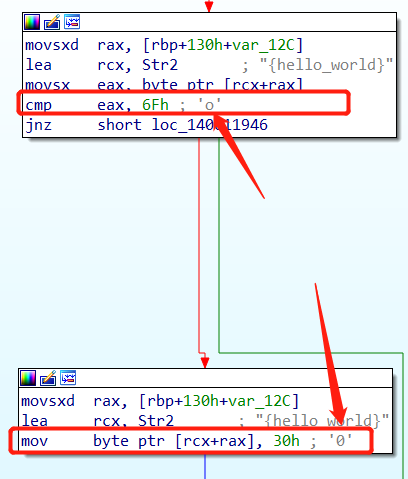
如何基于IDA对相关跳转进行修改

eg: jnz -> jz

利用16进制进行修改，jnz对应的16进制为75，而jz对应的16进制为74，对应到16进制界面，然后右键edit，修改完继续apply change。

修改完相应代码片段，保存为执行文件

Edit -> Patch program -> Apply patches to input file

230207

再探强网拟态密码学cry1

重新又看了一下这道题，感觉没必要利用原有的加密函数进行解密再进行操作。

主要把flag分成了两部分，而第一部分用简单数学推导也是可以直接把相关量给求解出来。

part1

原：利用源代码中的加密逆向写解密算法，中国剩余定理

现：费马小定理进行数学推导

已知：
$$
g_1 = g^{(p-1) \cdot r_1}\mod p
$$

$$
c_1 \equiv (m \times g_1^{s_1} \mod N )\mod N
$$

推导：主要利用费马小定理。
$$
g_1 = g^{(p-1)\cdot r1} \mod p \equiv 1
$$

$$
\Longrightarrow g_1 - 1 = k\cdot p
$$

而$N = p \times q$，所以此时，$p = gcd(g_1 - 1, N)$
$$
c_1 \equiv (m \times g^{s_1 \cdot r_1 \cdot (p-1)} \mod p) \mod N\
\Longrightarrow c_1 \equiv m \mod N
$$
所以，理论上$m \equiv c_1 \mod N$，但$N$范围太大了，基于$m$的长度不会太大，所以我们进行放缩处理，取$min (m \equiv c_1 \mod p, m\equiv c_1 \mod q)$.

最后推断出，实际上的$m$应为$c_1 \mod p$。

1
2
3

p1 = gcd(g1-1, N)
q1 = N // p1
m = c1 % p1

part2

原：Groebner basis相关知识点【还没搞懂。

现：转换成三元二次方程进行求解

先开$e$次方求出关于$ABC$的二次方程。再用roots()进行相应的求解。

题目中的$ABC$方程保持不变

cnt = len(Cs)
A = [(i + 128)**2 for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
C = [(i + 512) for i in range(cnt)]

对输出的$Cs$进行开$e$次方处理

1
2
3

C_ = []
for i in Cs:
    C_.append(iroot(i, Cs)[0])

定义在整数环上的未知变量$m1,m2,m3$

1
2
3

P.<m1> = Zmod()[]
P.<m2> = Zmod()[]
P.<m3> = Zmod()[]

分别代入原方程中，得到关于$ABC$的二次方程

1
2
3

f1 = A[0] * m1 ** 2 + B[0] * m1 + C[0] - int(C_[0])
f2 = A[1] * m2 ** 2 + B[1] * m2 + C[1] - int(C_[1])
f3 = A[2] * m3 ** 2 + B[2] * m3 + C[2] - int(C_[2])

求根，代值，再转换

v1 = f1.roots()
v2 = f2.roots()
v3 = f3.roots()

flag2 = long_to_bytes(v1[0][0]).decode() + long_to_bytes(v2[0][0]).decode() + long_to_bytes(v3[0][0]).decode()

分享-代码审计

CLTopen6.0

网上资产相对较多，代码审计相关。

审计application目录。

敏感数据，先搜索username之类的。查看数据库相关的表结构。

callback传参相关，可能存在XSS攻击。

方法是public的才可以进行调用。跟Java会比较相关或说类似？

准备

利用Seay等工具先进行代码审计，主要为了找到后台以及一些危险函数。

主要三个工具：

Seay辅助审计
phpstudy搭环境
psphp编辑器

调用

直接在地址栏访问类以及方法。
访问成功后，选择参数进行传参。
注意伪静态。

目录穿越？

不存在的目录影响payload的执行结果，从而影响命令的执行。

linux跟windows执行结果可能不同。

上传脚本

执行错误，但可以写入public目录。

但需要查看一下关键代码有没有错误，容易被过滤导致上传脚本操作失败。

及时恢复，否则前台可能出现问题。

阅读代码的能力还是非常重要的。主要还是得了解函数的具体作用，以及大概的实现流程是怎样的。

linux中Type = ../

因为涉及路径以及绕过等，所以感觉跟命令执行还是结合起来的。以及时刻记得恢复，否则容易挂。

空了可以尝试一下。稍微熟悉一下审计的流程。

总结

相对比较容易。

简单的相对来说就是来看敏感函数。

230208

Groebner basis

本子。

空闲整理。

Grobner basis简单讲就是两种算法的扩展延伸：Division algorithm 从单变量到多变量，Gaussian elimination从线性到非线性。

应用方面首先当然是解多变量多项式，其次还可以用于解决ideal membership problem：给你一个理想I，和一个多项式f，I的Grobner basis能告诉你f是否属于I。

Grobner basis算法是多变量密码核心问题。多变量密码的公钥就是一组有限域上多变量二次多项式。如果你能解开这组多项式方程组，那么你就能假冒签名，读取加密信息了。应用上没人会用BuchBerger算法来找Grobner basis。因为效率太低了，而且其中很多计算是浪费的。常用的是F4和F5算法。

sage

groebner_basis()

定义多变量的多项式环
利用定义好的多项式环构建一个Ideal
调用sage中的函数

稀奇古怪的概念

伞形曲面，又称惠特尼伞形面（Whitney umbrella）

u, v = var('u,v')
fx = u*v
fy = u
fz = v^2
parametric_plot3d([fx, fy, fz], (u, -1, 1), (v, -1, 1),frame=False, color="yellow")

KCTF2021秋，第十一题图穷匕见

[原创]KCTF2021秋第十一题图穷匕见 writeup-CTF对抗-看雪论坛-安全社区|安全招聘|bbs.pediy.com (kanxue.com)

230209

继续整活Groebner basis以及Polynomial

图穷匕见

babyrsa

DASCTF-NOVX

sage函数等

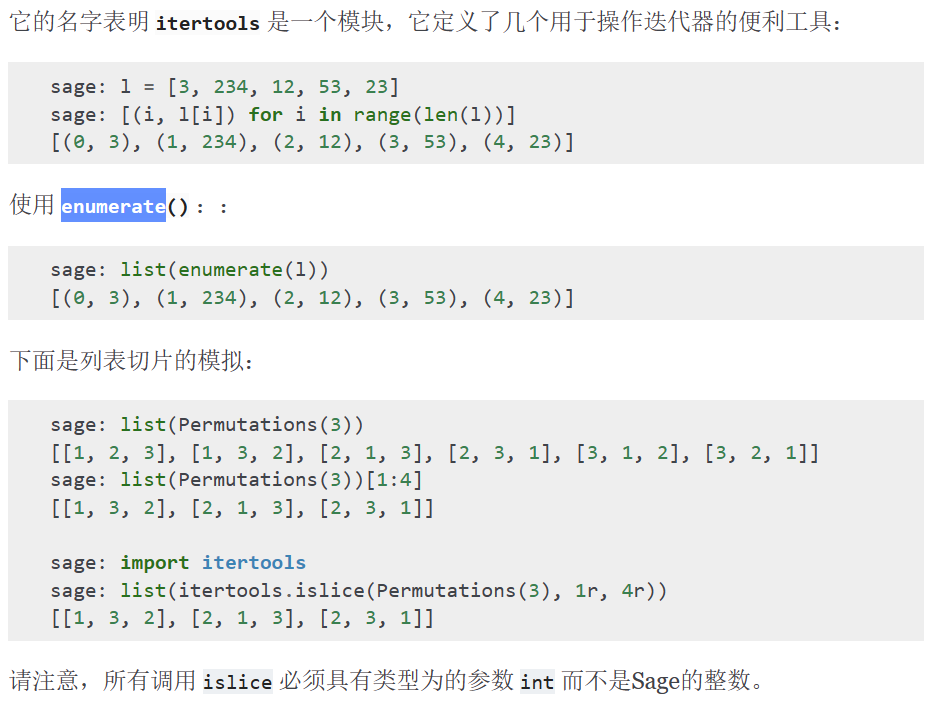
enumerate()

迭代工具，类似python中itertools模块

factor_list()

# poly
17358416697006*x^15 + 50380288275413*x^14 + 65697715730413*x^13 + 119331879197637*x^12 + 190079269759081*x^11 + 251069112740272*x^10 + 294191461464860*x^9 + 323192668237103*x^8 + 348744847375959*x^7 + 327797569086986*x^6 + 281393100562123*x^5 + 205257017269623*x^4 + 147796447331070*x^3 + 92272297080147*x^2 + 44365143036564*x + 12197084000688
poly.factor_list()
sage: p
39978*x^5 + 4693*x^4 + 11578*x^3 + 36393*x^2 + 14946*x + 43777
sage: q
26089*x^5 + 12232*x^4 + 20416*x^3 + 26651*x^2 + 26160*x + 11919
sage: r
16643*x^5 + 38547*x^4 + 21632*x^3 + 22341*x^2 + 25740*x + 23376

230210

easyrsa

n = 86073852484226203700520112718689325205597071202320413471730820840719099334770
n2 = 77582485123791158683121280616703899430016469065264033598472741751344256774648355531493586310864150337351815051848231793841751148287075688226384710343269278032576253497728407800522536152937473072438970839941923618053297480433385258911357458745700958378269978384670108026994918504237309072908971746160378531040480539649223970964653553804442759847964633088481940435582792404175653758785321463055628690804551479982557193366035172983893595403859872458966844805671311011033726279121149599533093604586152158331657286488305064843651636225644328162652701896037366058322959361248649656784810609391313
c3 = 260434870216758498838321584935711394249835963213639852217120194663627852693180232036075839403208332707552953757185774603238436545434522971149891312380970896040823539050341723863717581297624370198483155582245220695123793458717418658539983101802256991837534210806768587736557644192367876024337837658337683388449336720569707094997412847022794461117019613124291022681935875774139147643806772608929174881451749463825639214096129554621195116737322890163556732291246108250543079041977037626755130422879778449546701988814607595746282148723362288451970833214072743929855505520539885650891349827459470540263153862109871050950881032032388185414677989393461533362690744724752363346530211163516319373099647590952338730

"""
# 1. 分解n中的p, q
sage:
two_squares(n)
(200170033707580057053975766783012322797,
 214489650309129059054871357172058931331)
"""
p1 = 200170033707580057053975766783012322797
q1 = 214489650309129059054871357172058931331
q1 = q1 + 63066105847160076051036559850646146794

"""
# 2. 利用基底转换分解
poly = sum(e * x^i for i, e in enumerate( Integer(n2).digits(q1)))
sage: poly
17358416697006*x^15 + 50380288275413*x^14 + 65697715730413*x^13 + 119331879197637*x^12 + 190079269759081*x^11 + 251069112740272*x^10 + 294191461464860*x^9 + 323192668237103*x^8 + 348744847375959*x^7 + 327797569086986*x^6 + 281393100562123*x^5 + 205257017269623*x^4 + 147796447331070*x^3 + 92272297080147*x^2 + 44365143036564*x + 12197084000688

(p, _), (q, _), (r, _) = poly.factor_list()
sage: p
39978*x^5 + 4693*x^4 + 11578*x^3 + 36393*x^2 + 14946*x + 43777
sage: q
26089*x^5 + 12232*x^4 + 20416*x^3 + 26651*x^2 + 26160*x + 11919
sage: r
16643*x^5 + 38547*x^4 + 21632*x^3 + 22341*x^2 + 25740*x + 23376

 p, q, r = p(x = q1), q(x = q1), r(x = q1)
sage: assert p*q*r == n2
sage: p1
200170033707580057053975766783012322797
sage: p
65852498339760915228594889597136378107876107334695562152983809050259001488139010835535729480582643283480229654777004862320849604335829446520865511011593811440123502620735962409526109695434570356277
sage: q
42974281584522050062504679441184925920720278381761957641733614118720547476055402383959476142344396618643274705251619494499668048977089541037606316780609473959806621223833644762635231018066406261919
sage: r
27414656307685249691067705927388582241684529669740981719565564735302197575673076783872355553268011939023273356472727941960439764826793614011976095106476097211511966378338911454193294048309326195251
"""
p = 65852498339760915228594889597136378107876107334695562152983809050259001488139010835535729480582643283480229654777004862320849604335829446520865511011593811440123502620735962409526109695434570356277
q = 42974281584522050062504679441184925920720278381761957641733614118720547476055402383959476142344396618643274705251619494499668048977089541037606316780609473959806621223833644762635231018066406261919
r = 27414656307685249691067705927388582241684529669740981719565564735302197575673076783872355553268011939023273356472727941960439764826793614011976095106476097211511966378338911454193294048309326195251

"""
3. 根据原加密函数进行判断
"""
from gmpy2 import next_prime
while True:
    p1=next_prime(p1)
    p=next_prime(p)
    q=next_prime(q)
    r=next_prime(r)
    if (p-1)%7==0 and (q-1)%7 ==0 and (r-1)%7==0 and (p1-1)%7==0:
        break   

# print(p1)
# print(p)
# print(q)
# print(r)
        
"""
3. p域下解方程（flag未padding，在p域下可求解）
"""        
P.<x> = Zmod(p)[]
f = x^7 - c3
res = f.roots()
# print(res)
from Crypto.Util.number import *
for i in res:
    if b'DASCTF{' in long_to_bytes(int(i[0])):
        print(long_to_bytes(int(i[0])))

中间遇到判定没成功，也就是while true代码块没跑出结果，后来发现得用gmpy库中的next_prime()函数来加快。

VSC编译相关一点问题

主要安装编译之后生成的是64位的，编译好之后的程序文件是64位的，逆向后的显示有一点区别，稍微逆向查看伪代码以及汇编会相对麻烦一点。

VSC整个32位编译环境？

遗留问题

Windows环境之下如何编译成32位程序？
VSCode配置还原。或者说假设成功，那两者如何切换？

出题思路

思路来源，上面的图穷匕见。

crypto1

Feistel结构
Groebner basis方程
密码学题目也比较合适

230213

n2.digits(q2)——easyrsa

p, q, r = [gen_prime() for i in range(3)]
sage: p
7420106539
sage: q
16025170573
sage: r
15865175743

n2 = p * q * r
sage: n2.digits(13)
[9,
 12,
 1,
 1,
 11,
 10,
 10,
 2,
 2,
 6,
 2,
 5,
 3,
 11,
 12,
 3,
 12,
 4,
 12,
 12,
 5,
 5,
 6,
 6,
 4,
 7,
 7,
 1]

 for i,e in enumerate(n2.digits(13)):
....:     print(e * x^i)
....:
9
12*x
x^2
x^3
11*x^4
10*x^5
10*x^6
2*x^7
2*x^8
6*x^9
2*x^10
5*x^11
3*x^12
11*x^13
12*x^14
3*x^15
12*x^16
4*x^17
12*x^18
12*x^19
5*x^20
5*x^21
6*x^22
6*x^23
4*x^24
7*x^25
7*x^26
x^27

迭代器，以字典或者列表的形式进行输出。

sage: enumerate(n2.digits(13))
<enumerate object at 0x6ffe36f95550>
sage: list(enumerate(n2.digits(13)))
[(0, 9),
 (1, 12),
 (2, 1),
 (3, 1),
 (4, 11),
 (5, 10),
 (6, 10),
 (7, 2),
 (8, 2),
 (9, 6),
 (10, 2),
 (11, 5),
 (12, 3),
 (13, 11),
 (14, 12),
 (15, 3),
 (16, 12),
 (17, 4),
 (18, 12),
 (19, 12),
 (20, 5),
 (21, 5),
 (22, 6),
 (23, 6),
 (24, 4),
 (25, 7),
 (26, 7),
 (27, 1)]

(p, _), (q, _), (r, _) = poly.factor_list()
# 对poly多项式进行因式分解，使得得到p,q,r对应的多项式
# 此时p,q,r即为x = q1代入后的数值
p, q, r = p(x = q1), q(x = q1), r(x = q1)
assert p*q*r == n2

# 利用原加密函数得到真实的p1, p, q, r
from gmpy2 import *
while True:
    p1=next_prime(p1)
    p=next_prime(p)
    q=next_prime(q)
    r=next_prime(r)
    if (p-1)%7==0 and (q-1)%7 ==0 and (r-1)%7==0 and (p1-1)%7==0:
        break

# 这一模块无法计算出d，主要是因为原加密函数是经过判定才最终输出的。而判定为 -1 % 7。
# N = (p1 - 1)*(p1**2) * (p - 1) * (q - 1) * (r - 1)
# d = invert(mpz(e), mpz(N))
# print(d)

# 定义整数域模p的未知量x
# 在p域下求解方程
# 根为可能解，利用long_to_bytes()得到最终flag
P.<x> = Zmod(p)[] 
f = x^7 - c3 
res = f.roots() 
print(res)

easy_hash

根据myhash()函数，因为$a_0$的位数小于500位，所以$a_0$就是flag各个部分和其crc32()拼接后的结果，把crc32验证的结果去掉就是flag。

P = 93327214260434303138080906179883696131283277062733597039773430143631378719403851851296505697016458801222349445773245718371527858795457860775687842513513120173676986599209741174960099561600915819416543039173509037555167973076303047419790245327596338909743308199889740594091849756693219926218111062780849456373
a1, secret = (1768672211043417187765307394749760760531160781992300779145800061219666992833602547480090118225665457075744297987672863699370162614965380859290914620736, 89139545215288033432210221492974990584987914397112840989583439688211128705545477536596587262069032020212762581490561288493533363888589066045095054475929099275247145877699370608950340925139625068446642116123285918461312297390611577025368805438078034230342490499137494400676347225155752865648820807846513044723)

from Crypto.Util.number import *
from zlib import crc32

# 1. 原加密脚本的自定义函数保留下来
def myhash(x):
    res = []
    end = b""
    bytescipher = long_to_bytes(x)
    a = bytescipher[:len(bytescipher) % 8]
    res.append(a)
    res.append(long_to_bytes(crc32(a)))
    t = (len(bytescipher) // 8)
    bytescipher = bytescipher[len(bytescipher) % 8:]
    for i in range(t):
        a = bytescipher[i*8:i*8+8]
        res.append(a)
        res.append(long_to_bytes(crc32(a)))
    for i in res:
        end += i
    res = bytes_to_long(end)
    res = (res + (res >> 500)) & 2**(500) - 1
    return res

# def encode(pt):
#     a=[]
#     b=[]
#     a.append(myhash(pt))
#     for i in range(3):
#         a.append(myhash(a[i]))
#     for j in range(4):
#         secret=(a[0] + a[1] * a[j] + a[2] * a[j] ** 2 + a[3] * a[j] ** 3) % P
#         b.append([a[j],secret])
#     return b

# print(P.bit_length())

# 2. 利用a1来求解a2, a3
a2 = myhash(a1)
a3 = myhash(a2)

# 3. a0利用secret, a1, a2, a3求解
a0 = secret - (a1 * a1 + a2 * a1 ** 2 + a3 * a1 ** 3) % P
print(long_to_bytes(a0))

# 4. 把crc32部分去除，即可得到flag
# b'DA\xd4\x17\xe9\xf8SCTF{th1\x98\xf8\xa5$s_is_theS\x83\xbf\xc9_fe3st_q\x8f\xa9\xd4\xacuest1on}\x07.B\xce'
# b'DASCTF{th1s_is_the_fe3st_quest1on}'

references

some unread websites

(10条消息) 【zer0pts CTF 2022】 Anti-Fermat（p、q生成不当)_Paintrain的博客-CSDN博客_【zer0pts ctf 2022】anti-fermat

(10条消息) crypto_solveit2022（rsa中coppersmith攻击应用）_山猪儿烦不得的博客-CSDN博客

hackergame2020-writeups/README.md at master · USTC-Hackergame/hackergame2020-writeups · GitHub

(10条消息) DASCTF NOV X联合出题人2022年度积分榜争夺赛！Crypto Wp_dasctf nov x联合出题人2022年度积分榜争夺赛!_mxx307的博客-CSDN博客

Axiom Computer Algebra System (axiom-developer.org)

230214

窗口程序逆向思维

以Test_A_Windows为例

主程序入手
API入手

直接Shift + F12，打开string界面，然后查看关键字符串。本程序无法看到关键字符串，可能经过了编码转换。
查看API调用。
1. 读取的窗体中的字符串，一般调用了GetWindowsText
2. 弹窗，一般调用了MessageBox
3. 后面的A表示使用的编码形式，ASCII
4. 按x查看调用情况，前往地址
5. 红色时，无法按F5，此时IDA并未识别
6. 定位，然后Create Function，再F5手动创建函数
7. 中间涉及到strcmp，跟内联优化结合起来，此时需要对数据的来源进行查看
8. 按A直接数值转化
Test_A2.exe主要出现问题：粗虚线为内联优化

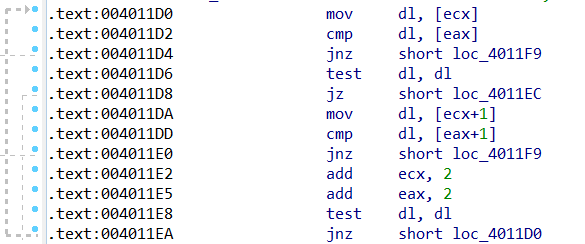
ecx拿取1字节放到dl中 <– 输入的字符串
eax拿取1字节放到dl中 <– 原存储字符串
dl与dl进行比较
一般2字节进行一次比较，然后进行循环，具体知识点看OneNote

然后真实需要的密钥就在内联优化的上面，稍微找一下。

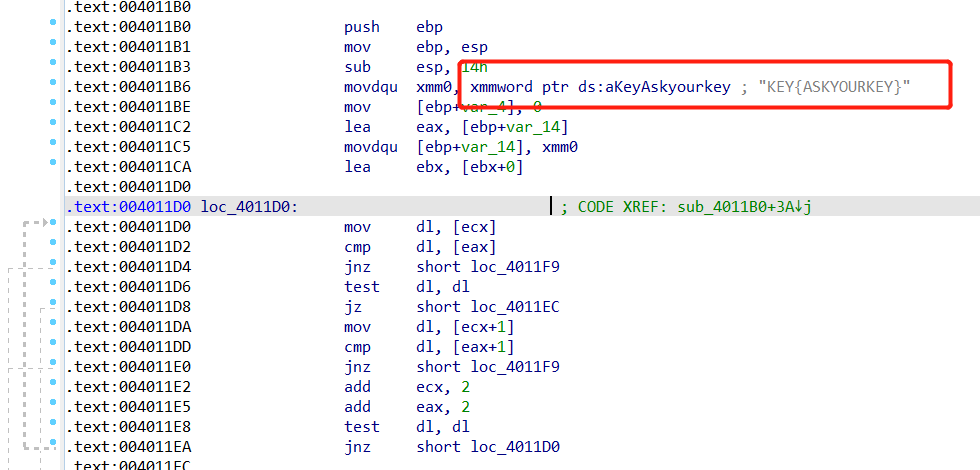
去原存储的地方进行转换一下即可，A

flag

内部的程序分析，分析过程进行整理。

230215

decode

古典密码学综合。

直接看ciphey感觉更直接。

凯撒13
base16/16进制转换
base64
ciphey直接得出

！

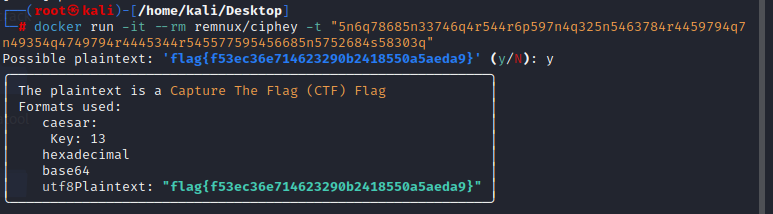
CakeRSA
逆向

230216

学习心得

学习笔记的编写

每周学习情况的汇总，有大致了解
知识点回顾，容易定位
有些问题，当时是遗留问题，后面可能又能解决了

密码学的数学推导

dp变种
- 扩展1：$n \equiv p^{b} \cdot q $
羊城杯Power
- dp扩展
- 数学推导，关键公式
拟态的再复现
- 多项式问题 -> 多元方程组问题
- 数学推导

-> 数学推导：费马小定理，简化本来比较复杂的等式。

-> 多项式相关

逆向相关基础以及工具运用

主要还是需要把基础知识点应用实际。

前提环境搭建
简单逆向题目复现
结合内联优化后的题目
- TEST_A2
偶然看到的结合密码学算法的逆向题目
- 逆向考查难题，容易跟密码学进行结合
- 逆向需要把变量/数据的变化过程了解

-> C语言以及多分析

-> 逆向技术学习论坛：看雪/吾爱破解（工具包）

遗留问题

一些docker靶场环境无法运行等 -> 明天试下docker看能不能直接运行
VSCODE，如何编译出32位程序文件
多项式相关定理学习

230217

分享后的遗留问题解决

docker在尝试中
VSCode，如何编译出32位程序文件仍待解决
1. 可替代方案：使用VS选择debugger进行
多项式定理，下周空了整吧

sqlmap重安装

报错了一堆问题，感觉是用的源有问题，先准备重新安装了
来来回回整活apt-get更新，回滚错误，麻爪了
事实证明还是得记得打个快照，kali彻底玩崩了。我去。
win7的父快照被我删没了，环境崩了。

俩环境都废了，自闭了，毁灭吧世界。

[qwb-2021-misc]threebody

用图片讲一个故事——第五届强网杯Threebody题目官方题解-安全客 - 安全资讯平台 (anquanke.com)

stegsolve查看发现图片

你们都是虫子。

放大发现像素点数

相邻像素点数值相差较大。

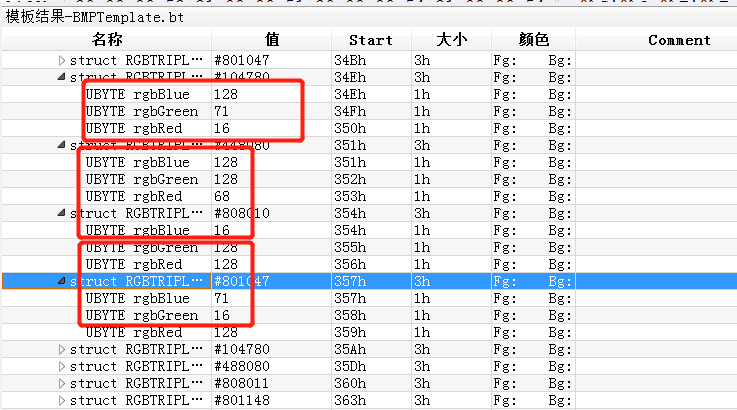
仔细观察发现如果以4为周期相差像素点数值将相差不大。 -> 修改像素点所占比特数biBitCount 24 -> 32

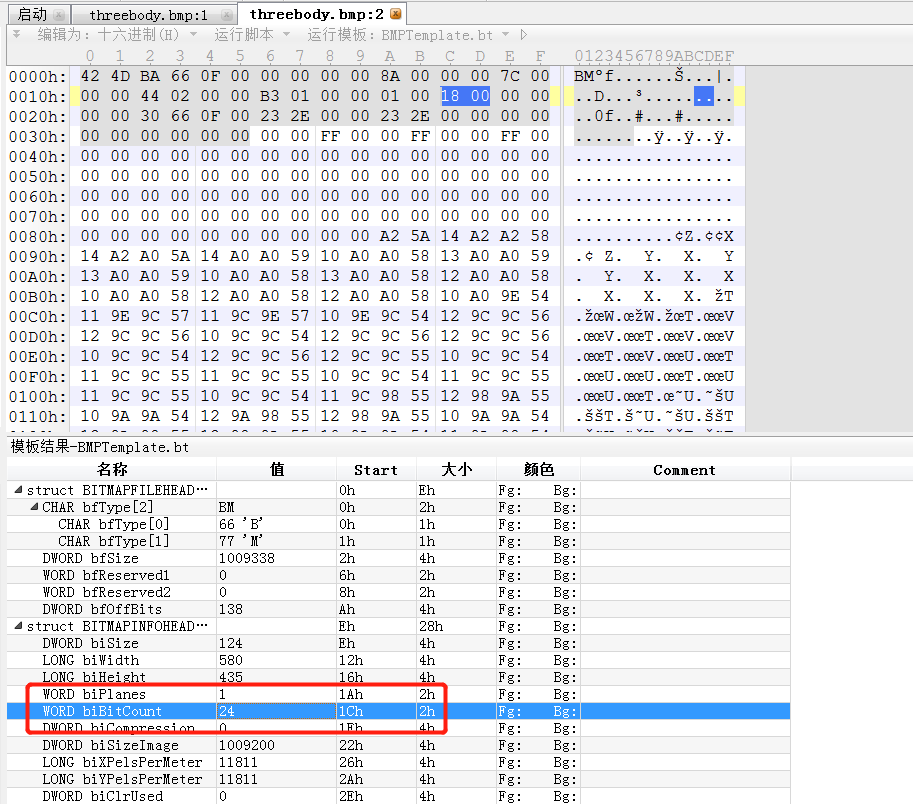
得到真实图片。

再使用solvesolve进行分析

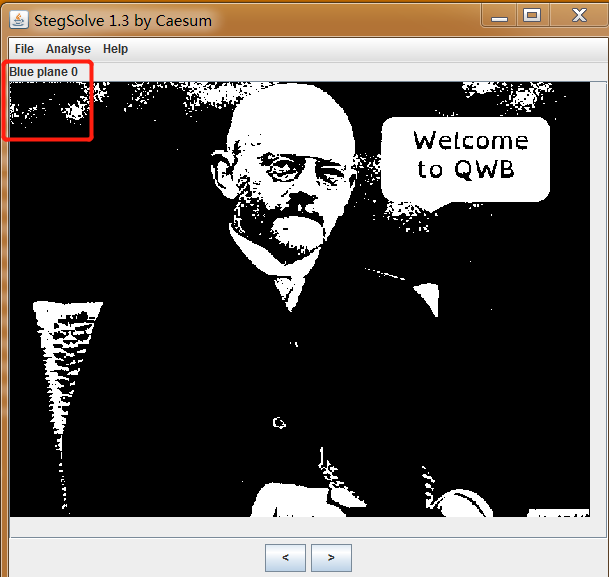
stegsolve进行提取。行列都存在隐写数据。

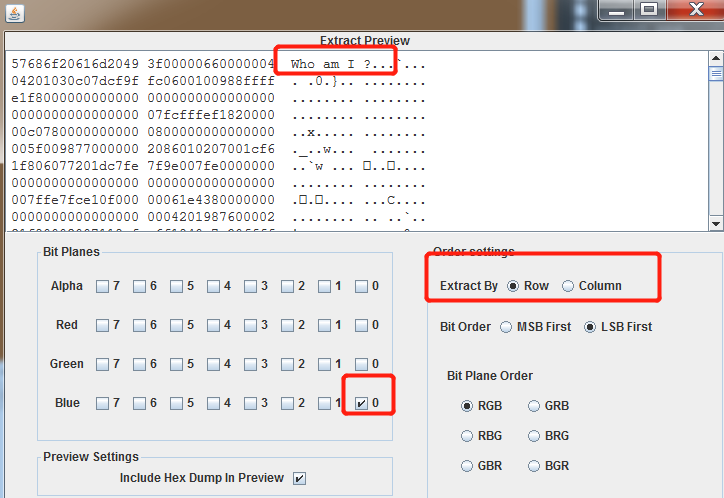
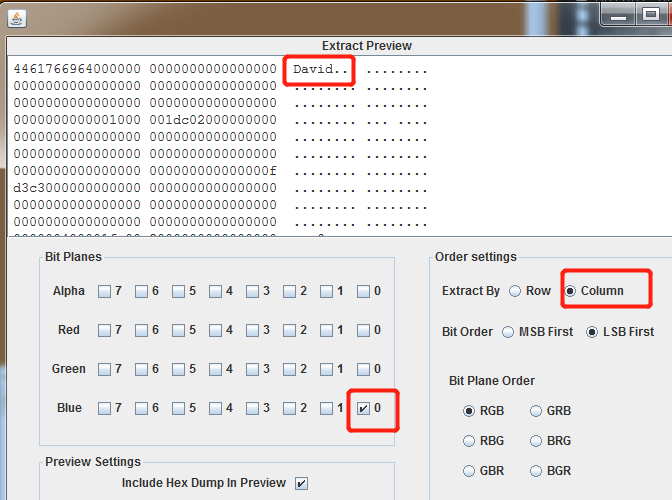
可得提示希尔伯特曲线

冗余数据赋值

观察图片发现存在rgbReserved的字段，表示stegsolve还存在无法识别的通道。

两种方法。

bmp转化成png
blue通道跟Reserved通道大小相近，直接暴力赋值

bmp转化成png

from PIL import Image
image=Image.new(mode='RGBA',size=(580,435))
with open(r'threebody.bmp','rb') as f:
    file=f.read()
    index=0
    for i in range(434,-1,-1):  #根据bmp的结构知道该bmp文件上下倒序存储像素值
        for j in range(0,580):
            s=[]
            for t in range(0,4):
                s.append(file[index])
                index+=1
            image.putpixel((j,i),(s[2],s[1],s[0],s[3]))  #
    image.show()
    image.save('threebody_new.png')

暴力赋值

with open('threebody.bmp', 'rb') as f:
    d = f.read()

w = 580
h = 435
b = 4
l = bytearray(d)
off = l[10]
for i in range(h):
    for j in range(w):
        l[off+j*b+i*b*w] = l[off+j*b+i*b*w+3]

with open('threebody_new.bmp', 'wb') as f:
    f.write(l)

希尔伯特曲线

reference: 真·降维打击！《三体》中二向箔吞噬地球的场景成真了！这位B站Up主过于硬核…… (qq.com)

import numpy as np
from PIL import Image
#安装：pip install -i https://pypi.tuna.tsinghua.edu.cn/simple hilbertcurve
from hilbertcurve.hilbertcurve import HilbertCurve
#提取像素数据
with Image.open('threebody_new.png') as img:
    arr = np.asarray(img)
arr = np.vectorize(lambda x: x&1)(arr[:,:,2])
#确定图片中的有效区域
for x1 in range(np.size(arr,0)):
    if sum(arr[x1])>0:
        break
for x2 in reversed(range(np.size(arr,0))):
    if sum(arr[x2])>0:
        break
for y1 in range(np.size(arr,1)):
    if sum(arr[:,y1])>0:
        break
for y2 in reversed(range(np.size(arr,1))):
    if sum(arr[:,y2])>0:
        break
#剪切出有效二维数据
arr = arr[x1:x2+1, y1:y2+1]
#print(x2+1-x1)#得出是128*128的矩阵
#构建希尔伯特曲线对象
hilbert_curve = HilbertCurve(7, 2)
#生成一维的二进制流数据
s = ''
for i in range(np.size(arr)):
    [x,y] = hilbert_curve.point_from_distance(i)
    s += str(arr[127-y][x])
#转ASCII文本写入文件
with open('output', 'wb') as f:
    f.write(int(s,2).to_bytes(2048, 'big'))

但这个一直没能实现，不清楚是不是没剪切图片的原因。

0228，笑死，真的是因为没剪切的原因。

C语言编译

打开output.txt发现是C语言脚本，所以用VSCode进行编译运行，发现打印的是自身。

出题人的知识点：

这种可以打印自身的程序学名叫Quine

即使看似是相同的文件，可能存在某种差异，直接用BCompare4对原始文件以及输出文件进行对比，发现在文件的第11行存在差别。

原始文件存在Tab以及Space，转化成01数据流。

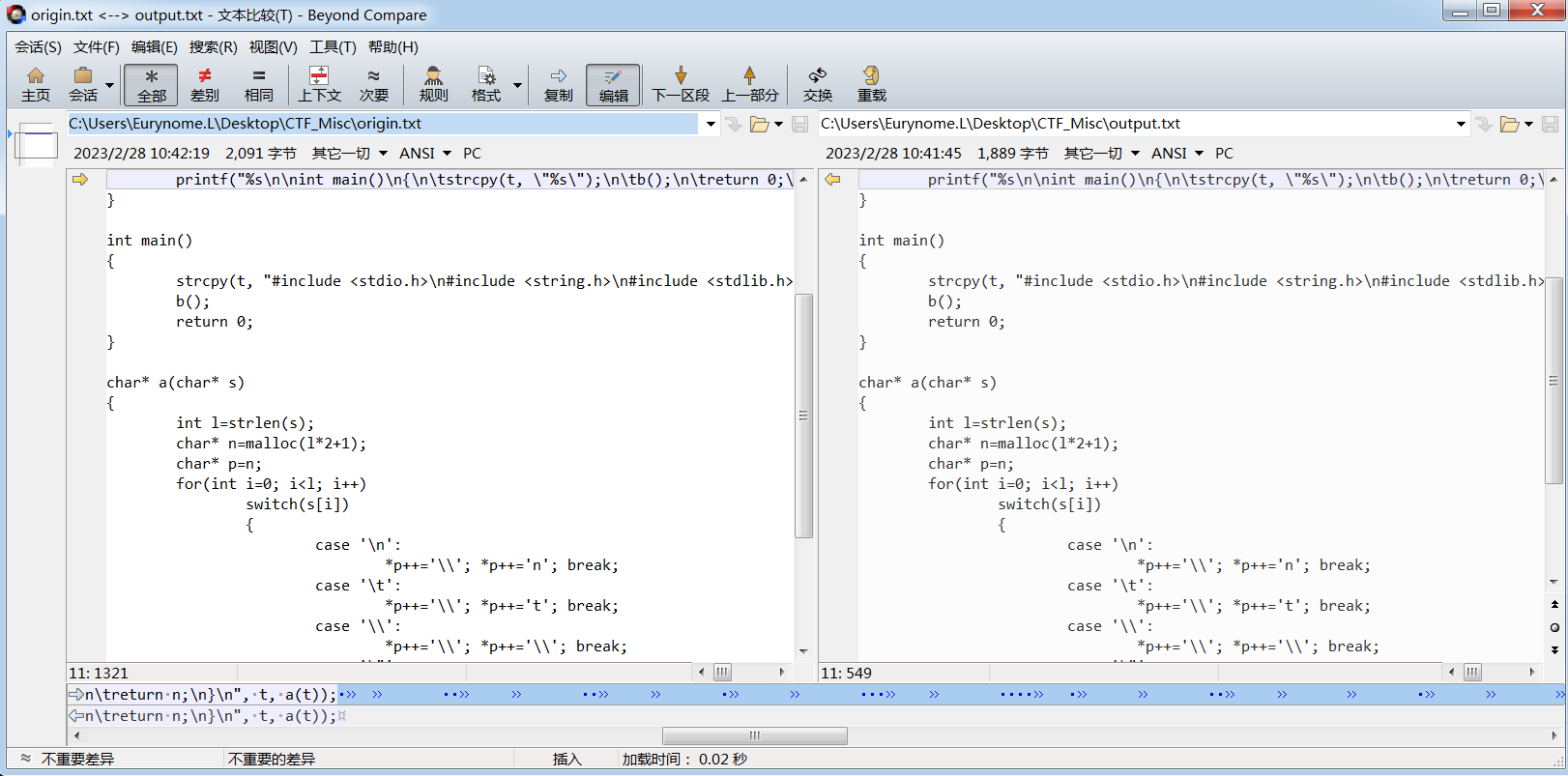
用Notepad++得到01数据流。

01100110011011000110000101100111011110110100010000110001011011010100010101101110001101010110100100110000011011100100000101101100010111110101000001110010001100000011011000110001011001010110110101111101

数据处理

output = '2009092020090920200909200909202020090920202020092009092020090909200909090920090920092020200920202020090920202009200909200909200920092020200920092009092009090920202009092009200920090920092020092020090920202020200909200909092020092020202020092009092009092020200920090909090920092009202020202009090920200920202009092020202020200909200909202020090920202009200909202009200920090920090920092009090909092009'
import re
output = output.replace('20', '0').replace('09', '1')
# print(output)
# 01100110011011000110000101100111011110110100010000110001011011010100010101101110001101010110100100110000011011100100000101101100010111110101000001110010001100000011011000110001011001010110110101111101
a = re.findall(r'.{8}', output)
flag = ''
for i in a:
    flag += ''.join(chr(int(i, 2)))
print(flag)
# flag{D1mEn5i0nAl_Pr061em}

230220

安装kali

本来还打算看下有无备用虚拟，后来下载，放弃了挣扎，算了，重新搭个环境吧。

Index of /virtual-images/current/ (kali.download)

配置kali相关环境

修改国内源以及更新

sudo vim /etc/apt/sources.list
国内源

# 官方源
# deb http://http.kali.org/kali kali-rolling main non-free contrib
# deb-src http://http.kali.org/kali kali-rolling main non-free contrib
#根据需要自己选一个，中科大的还可以
#中科大
deb http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib
deb-src http://mirrors.ustc.edu.cn/kali kali-rolling main non-free contrib
#阿里云
#deb http://mirrors.aliyun.com/kali kali-rolling main non-free contrib
#deb-src http://mirrors.aliyun.com/kali kali-rolling main non-free contrib
#清华大学
#deb http://mirrors.tuna.tsinghua.edu.cn/kali kali-rolling main contrib non-free
#deb-src https://mirrors.tuna.tsinghua.edu.cn/kali kali-rolling main contrib non-free
#浙大
#deb http://mirrors.zju.edu.cn/kali kali-rolling main contrib non-free
#deb-src http://mirrors.zju.edu.cn/kali kali-rolling main contrib non-free
#东软大学
#deb http://mirrors.neusoft.edu.cn/kali kali-rolling/main non-free contrib
#deb-src http://mirrors.neusoft.edu.cn/kali kali-rolling/main non-free contrib
#重庆大学
#deb http://http.kali.org/kali kali-rolling main non-free contrib
#deb-src http://http.kali.org/kali kali-rolling main non-free contrib

更新
- apt-get update更新索引
- apt-get upgrade更新软件
- apt-get dist-upgrade升级
- apt-get clean删除缓存包
- apt-get autoclean删除未安装的deb包

vmtool?

先将vmtools的压缩包拖到桌面，然后直接进行解压缩安装

tar zxvf VMwareTools-10.2.5-8068393.tar.gz
./vmware-install.pl

reboot

查看python2/3，并安装相关库

python2.7.18
python3.11.1

gmpy2

安装相关依赖库

# gmp库
apt-get install libgmp-dev
# mpfr库
apt-get install libmpfr-dev
# mpc库
apt-get install libmpc-dev

？pip2/pip3

pip2安装
- wget https://bootstrap.pypa.io/pip/2.7/get-pip.py
- python2 get-pip.py
但安装完之后无法调用，合理怀疑是这一部分出现相应问题，应该是没写入路径的问题

再安装又活了

环境变量

1
2
3

vim ~/.zshrc
# 在最后一行写入
export PATH=$PATH:/home/kali/.local/bin

ok，整活。

230306放弃挣扎，直接管理者模式进行安装相关库操作

？zsh

命令行出现zsh相关报错，具体解决方法如下所示。

cd ~
mv .zsh_history .zsh_history_bad
strings -eS .zsh_history_bad > .zsh_history
fc -R .zsh_history

pycryptodome

pip3 install pycryptodome

outguess

到对应目录下，直接使用outguess相关命令。

之后会提示没有安装，那就按它意思安装即可。

zsteg

管理员权限进入对应的目录之下。

然后运行gem install zsteg即可。

ciphey

安装https证书

apt-get install -y apt-transport-https ca-certificates

安装docker

apt-get install docker.io

验证docker

1
2
3

docker -v
systemctl start docker
docker ps -a

！安装ciphey

docker pull remnux/ciphey

目前可用且成功的命令：

docker run -it --rm remnux/ciphey -t [cipher]

-f [filename]不知道为啥一直不成功，暂且先放着看看。

TBC

但一时半会好像没啥需要测试查看的，暂且先放着吧。

230221

BlindWatermark

Releases · ww23/BlindWatermark · GitHub

安装windows-x86_64.jar
单水印图提取盲水印

Usage: java -jar BlindWatermark.jar <commands>
    commands:
        encode <option> <original image> <watermark> <embedded image>
        decode <option> <original image> <embedded image>
    encode options:
        -c discrete cosine transform
        -f discrete fourier transform (Deprecated)
        -i image watermark
        -t text  watermark
    decode options:
        -c discrete cosine transform
        -f discrete fourier transform (Deprecated)
    example:
        encode -ct input.png watermark output.png
        decode -c  input.png output.png

注意使用的算法，-c离散余弦变换，-f离散傅里叶变换

encode
- java -jar BlindWatermark.jar encode -ct[-ft/-ci/-fi] [] []
decode
- java -jar BlindWatermark.jar decode -c[-f] []

Rolan

AKA. ctftoolkit

理论出题

打算主要从《网络协议本质论》查找。

230224

修改白天黑夜模式

trial-1

为hexo next8.0主题添加一个可以切换的黑色/夜间模式 | Vince’s Blog (haomingzhang.com)

_config.next.yml

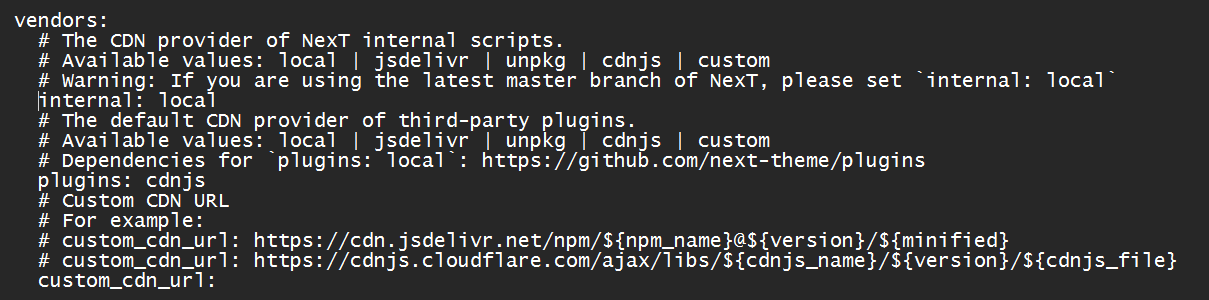
vendors.njk

{%- if theme.canvas_ribbon.enable %}
  <script size="{{ theme.canvas_ribbon.size }}" alpha="{{ theme.canvas_ribbon.alpha }}" zIndex="{{ theme.canvas_ribbon.zIndex }}" src="{{ theme.vendors.canvas_ribbon.url }}"></script>
{%- endif %}

{%- for name in js_vendors() %}
  {{ next_vendors(name) }}
{%- endfor %}

试了没成功，直接变成空白带背景页面了。

trial-2

Hexo Next 8.x 主题添加可切换的暗黑模式 | Clay 的技术博客 (techgrow.cn)

hahaha也不行，直接网页都解析不出来了。

烦人，难道真得还整点前端知识？

新增folk me

layout.njk

headband模块增加

<a href="your url" class="github-corner" aria-label="View source on GitHub"><svg width="80" height="80" viewBox="0 0 250 250" style="fill:#fff; color:#151513; position: absolute; top: 0; border: 0; left: 0; transform: scale(-1, 1);" aria-hidden="true"><path d="M0,0 L115,115 L130,115 L142,142 L250,250 L250,0 Z"></path><path d="M128.3,109.0 C113.8,99.7 119.0,89.6 119.0,89.6 C122.0,82.7 120.5,78.6 120.5,78.6 C119.2,72.0 123.4,76.3 123.4,76.3 C127.3,80.9 125.5,87.3 125.5,87.3 C122.9,97.6 130.6,101.9 134.4,103.2" fill="currentColor" style="transform-origin: 130px 106px;" class="octo-arm"></path><path d="M115.0,115.0 C114.9,115.1 118.7,116.5 119.8,115.4 L133.7,101.6 C136.9,99.2 139.9,98.4 142.2,98.6 C133.8,88.0 127.5,74.4 143.8,58.0 C148.5,53.4 154.0,51.2 159.7,51.0 C160.3,49.4 163.2,43.6 171.4,40.1 C171.4,40.1 176.1,42.5 178.8,56.2 C183.1,58.6 187.2,61.8 190.9,65.4 C194.5,69.0 197.7,73.2 200.1,77.6 C213.8,80.2 216.3,84.9 216.3,84.9 C212.7,93.1 206.9,96.0 205.4,96.6 C205.1,102.4 203.0,107.8 198.3,112.5 C181.9,128.9 168.3,122.5 157.7,114.1 C157.9,116.9 156.7,120.9 152.7,124.9 L141.0,136.5 C139.8,137.7 141.6,141.9 141.8,141.8 Z" fill="currentColor" class="octo-body"></path></svg></a><style>.github-corner:hover .octo-arm{animation:octocat-wave 560ms ease-in-out}@keyframes octocat-wave{0%,100%{transform:rotate(0)}20%,60%{transform:rotate(-25deg)}40%,80%{transform:rotate(10deg)}}@media (max-width:500px){.github-corner:hover .octo-arm{animation:none}.github-corner .octo-arm{animation:octocat-wave 560ms ease-in-out}}</style>

pjax -> true

新增标题首字母大写形式

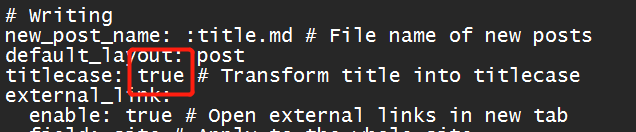
还在犹豫的功能集合

草稿以及各种模板

使用hexo new来建立文章会将新文章建立在 source/_posts 目录下，当使用 hexo generate 编译文件时，会将其 HTML 结果编译在 public 目录下，之后hexo server将会把 public 目录下所有文章发布。

hexo new draft <title>	# 新建草稿文章
hexo s --draft	        # 预览草稿文章
    
# 发布
hexo P <filename>   #不包含 md 后缀的文章名称

版权

在_config.next.yml文件内。

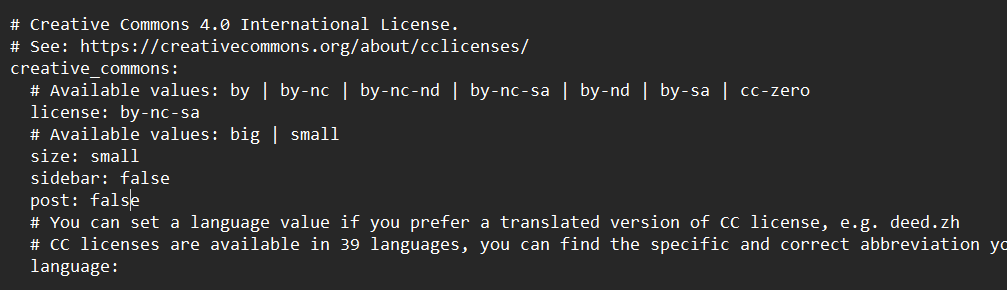
post为true时开启版权，相应的为false时关闭版权。

230228

threebody收尾

解决希尔伯特曲线运行不成功问题
想作为出题素材来，但目前逆向过去有点迷惑
但希尔伯特曲线可以作为出题一个知识点

python一些用法

replace(from, to)

# replace at the same time
output = '2009092020090920200909200909202020090920202020092009092020090909200909090920090920092020200920202020090920202009200909200909200920092020200920092009092009090920202009092009200920090920092020092020090920202020200909200909092020092020202020092009092009092020200920090909090920092009202020202009090920200920202009092020202020200909200909202020090920202009200909202009200920090920090920092009090909092009'
output = output.replace('20', '0').replace('09', '1')
print(output)
# 01100110011011000110000101100111011110110100010000110001011011010100010101101110001101010110100100110000011011100100000101101100010111110101000001110010001100000011011000110001011001010110110101111101

re库

(10条消息) 【Python 学习】基础知识（3）——re库_python语言中，re库_一碗萝卜头的博客-CSDN博客

函数	说明
re.search(pattern,string,flags=0)	在一个字符串中搜索匹配正则表达式的第一个位置，返回match对象
re.match(pattern,string,flags=0)	从一个字符串的开始位置起匹配正则表达式，返回match对象
re.findall(string[, pos[, endpos]])	搜索字符串，以列表类型返回全部能匹配的子串
re.split(string[, maxsplit])	将一个字符串按照正则表达式匹配结果进行分割，返回列表类型
re.finditer()	搜索字符串，返回一个匹配结果的迭代类型，每个迭代元素式match对象
re.sub(repl, string[, count])/re.sub(pattern, repl, string)	在一个字符串中替换所有匹配正则表达式的子串，返回替换后的字符串

pattern：匹配的正则表达式

string：要匹配的字符串

flags：标志位，用于控制正则表达式的匹配方式，如：是否区分大小写，多行匹配等等。

flags:

类别	描述
`re.I`	忽略大小写
`re.L`	表示特殊字符集 `\w`, `\W`, `\b`, `\B`, `\s`, `\S` 依赖于当前环境
`re.M`	多行模式
`re.S`	即为 `.` 并且包括换行符在内的任意字符（`.` 不包括换行符）
`re.U`	表示特殊字符集 `\w`, `\W`, `\b`, `\B`, `\d`, `\D`, `\s`, `\S` 依赖于 Unicode 字符属性数据库
`re.X`	为了增加可读性，忽略`空格`和 `#` 后面的注释

re.search(patten, string, flags = 0)

import re
s = 'hello_world_123'
print(re.search('ll', s))
# <re.Match object; span=(2, 4), match='ll'>

re.match(pattern,string,flags=0)

与re.search()的区别在于：
- re.match()是从起始位置就匹配成功，否则返回none;
- re.search()匹配整个字符串，直到找到一个匹配成功的。注意：一次匹配，如果后面还有匹配的也不会查找了.
提取数据：group
- group()用来提取分组截获的字符串，（）用来分组。
- group() 同group（0）用来表示匹配正则表达式整体结果。
- group(1) 列出第一个括号匹配部分，group(2) 列出第二个括号匹配部分
- group(3) 列出第三个括号匹配部分。
- 当嵌套分组时（有两层括号），即r'((expression1)(expression2))'的情况时，最外层的分组被解释成一个整体group(1)，里层的分组解释从group(2)开始
- 没有匹配成功的，re.search()返回None。

import re
s = 'hello_world_123'
print(re.match('he', s))
# <re.Match object; span=(0, 2), match='he'>
s = 'hello_world_123'
print(re.match('hl', s))
# None

除非首字符串符合，否则直接返回None

从一个字符串的开始位置起匹配正则表达式返回match对象。

常用方法：

方法	描述
group()	用于获得一个或多个分组匹配的字符串，当要获得整个匹配的子串时，可直接使用 group() 或 group(0)
span()	返回匹配字符串的起始位置
start()	用于获取分组匹配的子串在整个字符串中的起始位置（子串第一个字符的索引），参数默认值为 0
end()	用于获取分组匹配的子串在整个字符串中的结束位置（子串最后一个字符的索引+1），参数默认值为 0

re.findall(pattern,string,flags=0)

import re
s = 'hello_world_123'
print(re.findall(r'.{2}', s))
# ['he', 'll', 'o_', 'wo', 'rl', 'd_', '12']

可按字符数量进行分离，输出为列表形式，不满的直接舍去。

搜索字符串，以列表类型返回全部能匹配的子串

re.split(pattern,string,maxsplit=0,flags=0)

正则表达式中的符号

正则字符

正则符号	描述	示例
`\`	转义字符。例如， ‘n’ 匹配字符 ‘n’。
`（）`	标记一个子表达式的开始和结束位置。	``
`.`	匹配换行符`\n`之外的任何单字符	`\.`
`	`	`
`\d`	匹配字符串中的单个数字	等价于[0-9]
`\D`	匹配非数字，即不是数字
`a-zA-Z`	匹配全部英文字符
0-9	匹配全部数字
`\w`	单词字符	等价于[A-Za-z0-9]
`\W`	匹配非单词字符
`\s`	匹配字符串中的`\n`, `\t`, `空格`
`\S`	匹配非空白字符
`[]`	中括号内任意正则符号均可参与匹配	`[abc]`表示a、b、c，`[a-z]`表示a到z的单个字符
`[^]`	当在方括号表达式中使用，^对其后的正则表达式进行了反义表达	`[^abc]`表示非a或非b或非c的单个字符

限定字符

正则符号	描述	匹配自己时
`*`	匹配前面的子表达式0次或多次	`abc*`表示`ab`, `abc`, `abcc`……
`?`	匹配前面的子表达式0次或1次	`abc?`表示`ab`, `abc`
`+`	匹配前面的子表达式1次或多次	`abc+`表示`abc`, `abcc`, `abccc`……
`{m}`	m是一个非负整数，匹配确定的m次	`ab{2}c`表示`abbc`
`{m,}`	m是一个非负整数，至少匹配m次
`{m, n}`	m和n均为非负整数，其中$m\le n$，扩展前一个字符m至n次	`ab{1, 2}c`表示`abc`, `abbc`

定位字符

正则符号	描述	匹配自己时
`^`	匹配输入字符串的开始位置	`\^`
`$`	匹配输入字符串的结尾位置	`\$`
`\b`	匹配一个单词边界，即字与空格间的位置
`\B`	非单词边界匹配

经典案例

正则符号	描述
`^[A-Za-z]+$`	由26个字母组成的字符串
`^[A-Za-z0-9]+$`	由26个字母和数字组成的字符串
`^-?\d+$`	整数形式的字符串
`^[1-9][0-9]`	正整数形式的字符串
`[1-9]\d{5}`	中国境内邮政编码，6位
`[\u4e00-\u9fa5]`	匹配中文字符
`\d{3}-\d{8}	\d{4}-\d{7}`

230301

2-8 明码比较

9-16爆破

17-18内存分析

19-20逻辑分析

CTF++ 2

flag{a6145c1e440e9d30c861c53a07af6def}

前面的操作步骤跟Test_A2类似。（看0214的具体步骤）

经过分析，可溯源看到一些16进制字符串：

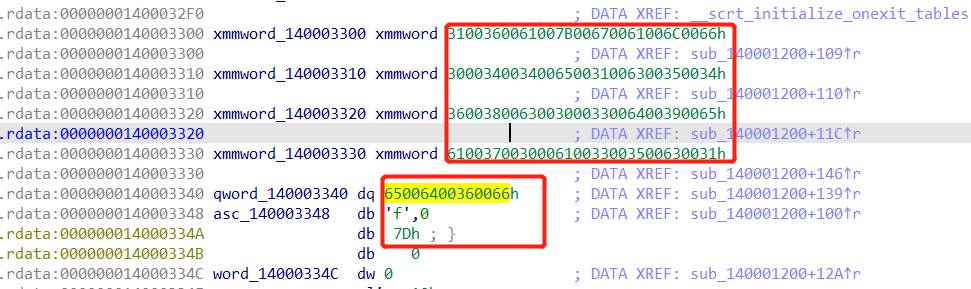
理论上直接把上边的字符串按A直接转换也可以得到相应的flag，但随时练习一下用代码处理这些字符串吧~

list0 = ['3100360061007B00670061006C0066', '300034003400650031006300350034', '360038006300300033006400390065', '610037003000610033003500630031', '65006400360066', '7D0066']
output = []
import re
for i in list0:
    output.append(re.findall(r'.{2}', i)[::-1])
# print(output)
# [['66', '00', '6C', '00', '61', '00', '67', '00', '7B', '00', '61', '00', '36', '00', '31'], ['34', '00', '35', '00', '63', '00', '31', '00', '65', '00', '34', '00', '34', '00', '30'], ['65', '00', '39', '00', '64', '00', '33', '00', '30', '00', '63', '00', '38', '00', '36'], ['31', '00', '63', '00', '35', '00', '33', '00', '61', '00', '30', '00', '37', '00', '61'], ['66', '00', '36', '00', '64', '00', '65'], ['66', '00', '7D']]
flag = ''
for i in output:
    for j in range(len(i)):
        if int(i[j], 16) != 0:
            flag += chr(int(i[j], 16))
    print(flag)
# flag{a6145c1e440e9d30c861c53a07af6def}

CTF++ 3

flag{0272995b2b6bbc4915f717c2562e8b39}

emm，直接看string界面就行了。

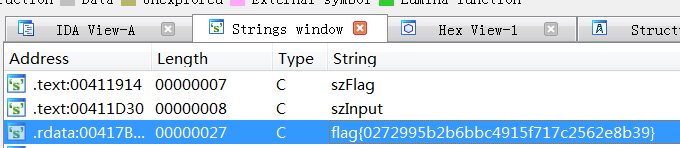
CTF++ 4

flag{0272995b2b6bbc4915f717c2562e8b39}

顺着流程图结合汇编语言大概分析一下，比较关键的地方就是下面红框所示，看下两个红框进行了比较处理等，说明是关键数据，直接到对应地方查看数据，然后将这些数据使用代码处理一下，得到相应的flag。

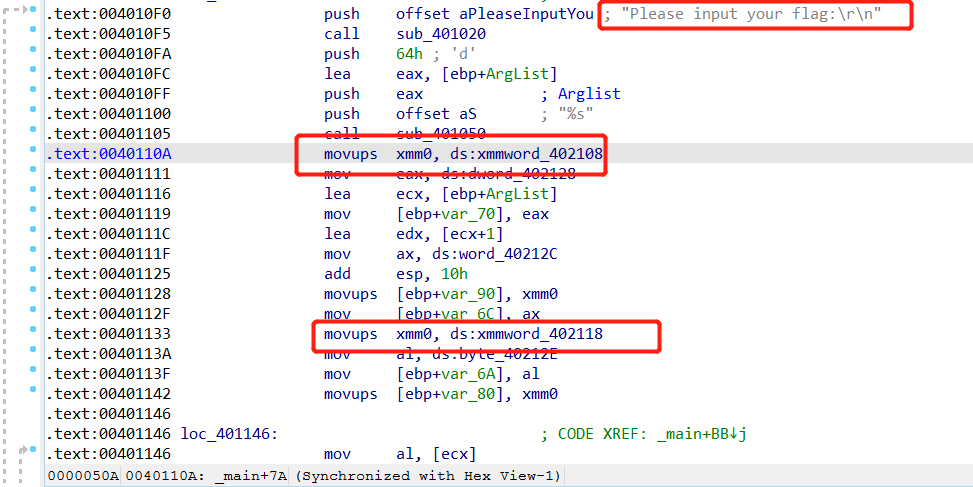
跳转到关键数据处。

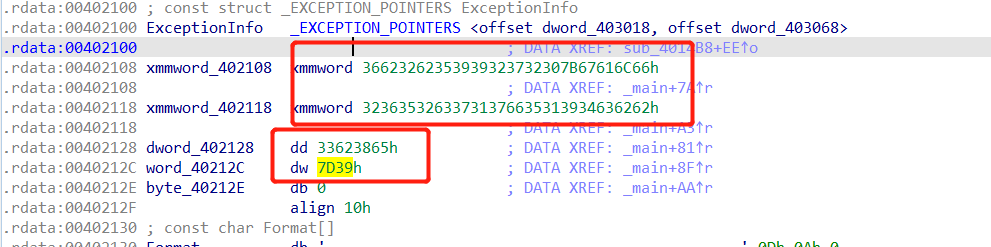
代码如CTF++ 3所示。

CTF++ 5

flag{0272995b2b6bbc4915f717c2562e8b39}

？？？

好像确实flag没变。

CTF++ 6

flag{a6145c1e440e9d30c861c53a07af6def}

前面步骤跟TEST_A类似。

中间跳转到调用函数的汇编语言处，会发现是红色的，所以上溯到函数入口，然后create function，再重新去对应地方，根据判断条件找到对应参数，然后跳转到对应参数去。

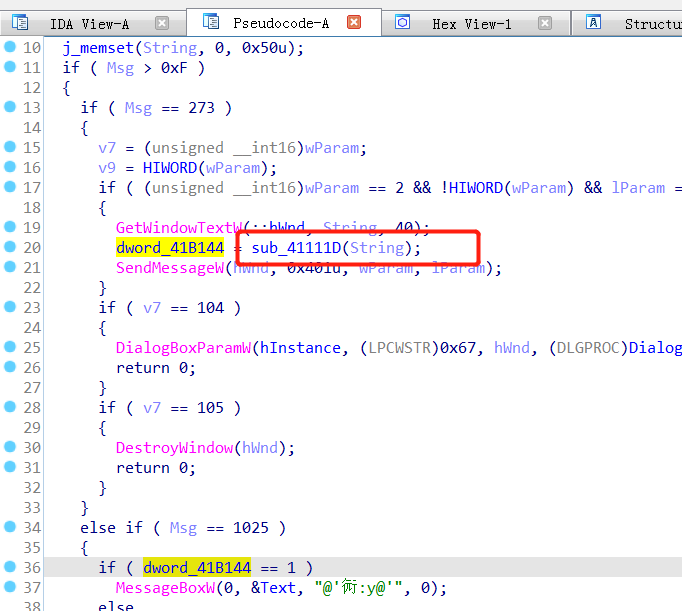
再进行跳转。

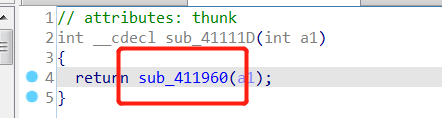
最后就直接到flag的地方了。

CTF++ 7

flag{a6145c1e440e9d30c861c53a07af6def}

emm，直接函数跳转就到了。

CTF++ 8

flag{a6145c1e440e9d30c861c53a07af6def}

跟6类似，一路跳转找到对应的参数即可。

脑子有点糊，不想搞，摸鱼了。

230302

github-token

9

Str：What_should_I_do

b3596e322275cb5e59a9a9f50a274715

果不其然错了，但觉得定位到key part了。

230303

(10条消息) CTF逆向总结（二）_沐一 · 林的博客-CSDN博客

9

flag{0272995b2b6bbc4915f717c2562e8b39}

关于修改汇编代码或者跳转逻辑

直接选定对应的汇编代码，然后选择Edit -> Patch Program -> Assemble，修改对应的汇编代码，如下图，jnz -> jz。

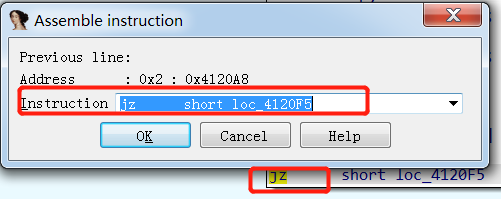
也可以到hex界面，修改对应的机器码，如jnz对应的机器码为75，然后修改机器码为74，即jz。

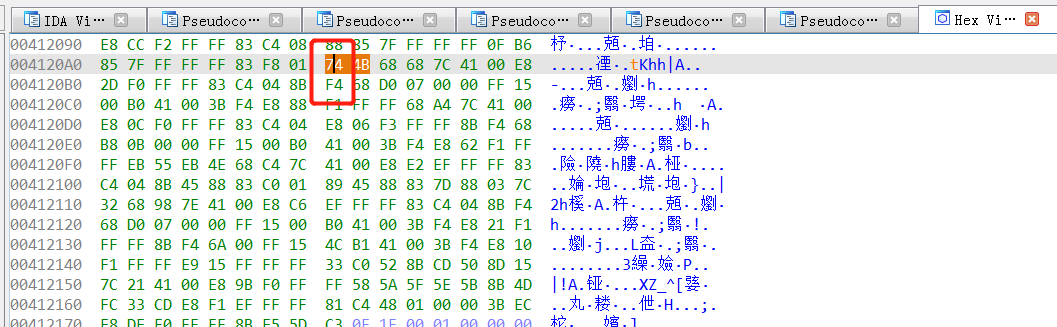
剩下步骤，如0206 0206-0210.md 所示。
生成新的执行文件后，就可以改变原有的跳转逻辑，即使输出错误也可以直接得到相应的flag了。

Test_B

两条路：

修改跳转逻辑
分析原始代码，直接爆破相关数据

10

flag{0272995b2b6bbc4915f717c2562e8b39}

逻辑一致了，直接把原本的判断条件以及跳转逻辑修改一下即可。

原本的判断条件是jz，并且运行之后是往错误的方向跳转，那我们直接修改一下当前的一个跳转逻辑即可成功运行到我们期望的正确路线运行。

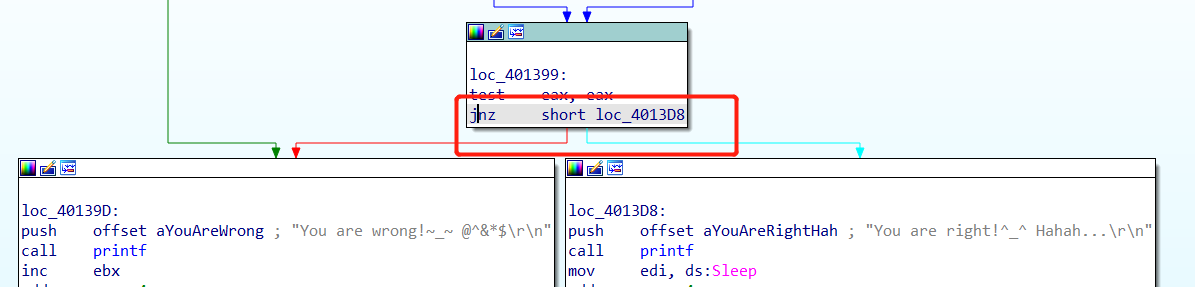
但这边分析也存在一点问题，原本在debug分析中能看到当前的数据，但release之后，无法看到当前的数据，如果打算走分析爆破的路线的话，这部分可能存在一点没注意到的地方。

11

flag{0272995b2b6bbc4915f717c2562e8b39}

思路同上，比较麻烦的一点是，难以跳转到验证条件的流程图。

定位的思路

先查看string界面，然后找到关键字符串you are rightetc.
跳转进入之后，找到该字符串对应的关键函数aYouAreRighthHah
定位到关键函数之后，直接按x查看交叉使用的地方
最终定位到流程图的调用界面了
再按需求进行相应地修改并应用

12

flag{0272995b2b6bbc4915f717c2562e8b39}

跟10类似。

13

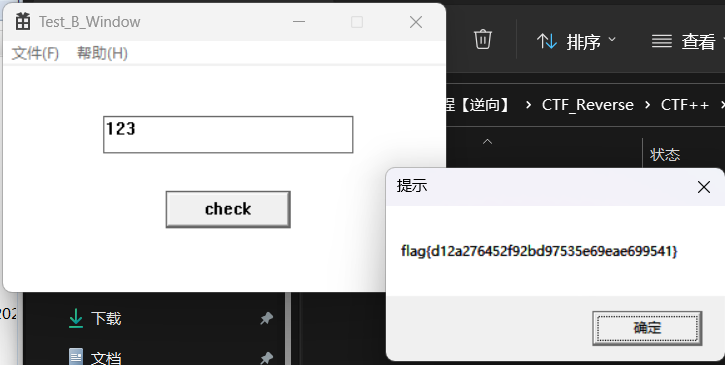
flag{d12a276452f92bd97535e69eae699541}

整体逻辑跟上面是类似的，经过窗口输入，发现输入错误直接跳转到了错误字段，那么我们同样把判断逻辑改变一下，直接跳转到给出flag部分，就可以直接得到flag了。

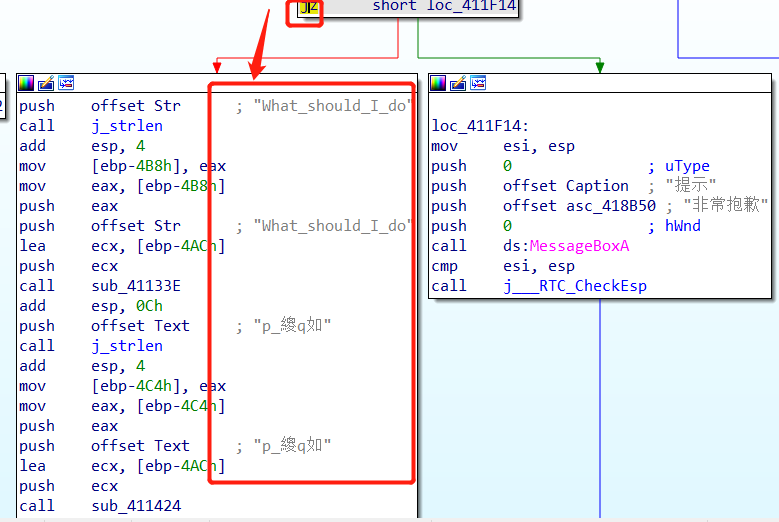
不行，心梗得难受，空了把C语言中涉及到RC4的加解密逻辑理顺一遍，

14

flag{d12a276452f92bd97535e69eae699541}

类似，关键还是得定位判定条件所处的位置。

230306

15

flag{d12a276452f92bd97535e69eae699541}

利用函数跳转到判定条件，修改重生成即可。

16

flag{d12a276452f92bd97535e69eae699541}

同上，定位判定的汇编语句。

kali安装vol

中间出现一点问题：

管理员模式以及当前模式下的pip2指向的路径不一样
construct模块一直安装不成功

当前解决：

直接干脆全用管理员模式的pip2进行相关安装库操作
setuptools没安装/没更新

gnuplot

安装

sudo apt-get install gnuplot

使用

txt文件，内含坐标
进入目录，运行gnuplot
后运行plot'xxx.txt'

但为啥导出的图片放到win7直接成一半了呢。

230307

kali爆破Linux密码

(10条消息) Kali 爆破 Linux 密码 | 使用 John the Ripper 爆破 etc/shadow 文件 | 报错： UTF-8 No password hashes loaded_kali 爆破目录_学习溢出的博客-CSDN博客

题目：

Crypto: Shadow – W3Challs Hacking Challenges

解答：

把需要爆破的放到一个文件
直接使用join进行爆破，sudo john /home/kali/Desktop/CRYPTO/task --format=crypt --wordlist=/usr/share/wordlists/rockyou.txt
最后得到root的密码

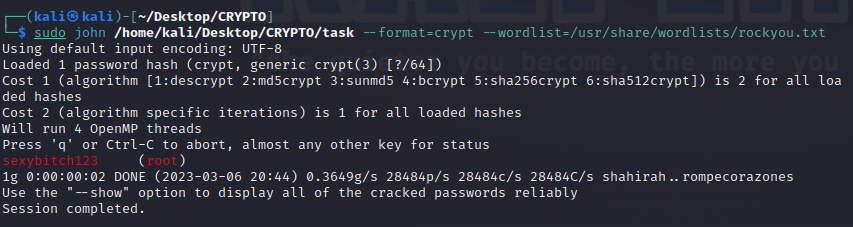
join的新使用

因为从 Debian 11 / bullseye 系统（适用于Kali）开始，默认的密码哈希函数使用 yescrypt 。
因此之前 John the Ripper 的命令将无法再运行。

1
2
3

sudo john [/etc/shadow] --format=crypt
sudo john [/etc/shadow] --format=crypt --wordlist=/usr/share/john/password.lst
sudo john [/etc/shadow] --format=crypt --wordlist=[../]rockyou.txt

在找到密码后，如果不小心关掉窗口了可以使用 --show 来再次显示已经爆破的密码。

1	sudo john [/etc/shadow] --show

F5算法环境修改

(10条消息) 安装F5-steganography和使用，及解决java环境版本报错问题_墨笙故君的博客-CSDN博客

Java指定版本下载

https://www.oracle.com/java/technologies/downloads/#java11，下载java11.0.18的压缩包

移动到指定路径并切换进行解压缩

1
2
3

mv jdk-11.0.18_linux-x64_bin.tar.gz /etc/opt
cd /etc/opt
tar -zxvf jdk-11.0.18_linux-x64_bin.tar.gz

拷贝解压后的Java文件至指定路径

1	cp -r jdk-11.0.18/ /usr/bin

安装并进行注册

update-alternatives --install /usr/bin/java java /etc/opt/jdk-11.0.18/bin/java 1
update-alternatives --install /usr/bin/javac javac /etc/opt/jdk-11.0.18/bin/javac 1
update-alternatives --set java /etc/opt/jdk-11.0.18/bin/java
update-alternatives --set javac /etc/opt/jdk-11.0.18/bin/javac

中间出现手动模式，好像不太影响整体的安装注册

查看切换后的Java版本

1	java --version

注册了Oracle，no \

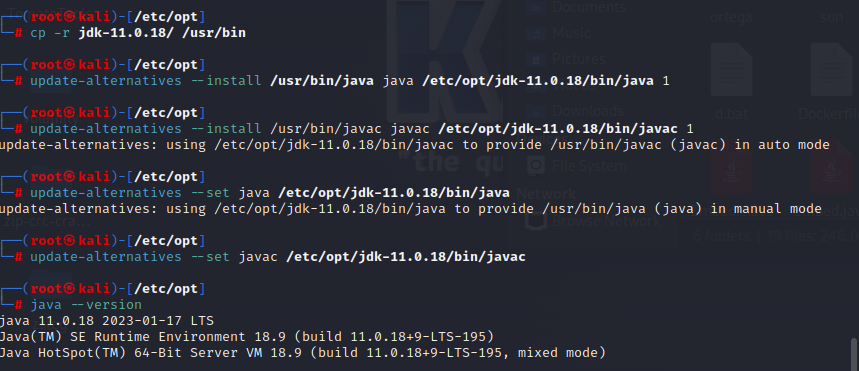
运行测试

最后再运行一下F5，输出为output.txt

！图像相关

https://lazzzaro.github.io/2020/05/06/misc-%E5%9B%BE%E5%83%8F%E5%A4%84%E7%90%86/

！网安练习平台

(10条消息) 国内外优秀网安练习平台_Ms08067安全实验室的博客-CSDN博客

！Hydra

Linux下暴力破解工具Hydra详解 - Merlin_Tang - 博客园 (cnblogs.com)

RC4，C语言代码分析以及python实现

char gszFlag[40] = {};
char cmpFlag[256] = { 0x70,0x5f,0xbf,0x8f,0x71,0x9c,0xe4,0xf0,0x4b,0x50,0x70,0x4f,0x7e,0x85,0xd8,0x7b,0x9e,0x5b,0xe1,0x60,0x04,0xf0,0xee,0x8b,0x08,0x1a,0xfb,0x69,0x60,0x2f,0x4e,0xa7,0x7e,0x92,0x4d,0xda,0x9a,0x36 };
char paswd[256] = { 0x52,0x5c,0xa7,0x87,0x7f,0xc7,0xb8,0xf7,0x0e,0x36,0x21,0x15,0x6b,0xc3,0xd5,0x3d,0x9d,0x4d,0xe1,0x3c,0x5c,0x9e,0xab,0x9f,0x50,0x4c,0xbe,0x6b,0x3f };
char rc4_key[256] = { "What_should_I_do" };

定义数组，不完全初始化以及完全初始化，未填满的部分全部为0

230308

【护网杯2018】easy_dump

###利用vol查看镜像信息

vol.py -f easy_dump.img imageinfo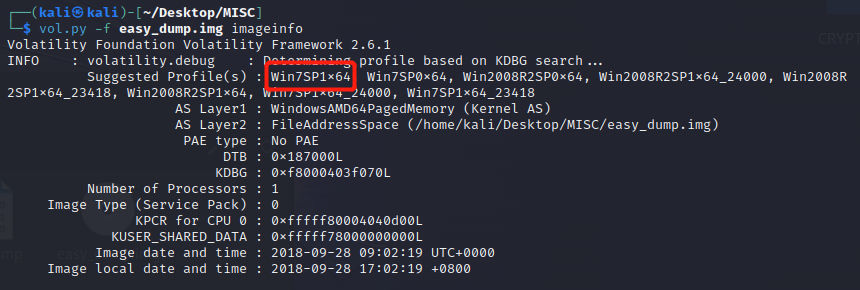

一般以镜像前1，2个操作系统为分析重点，eg: Win7SP1x64

指定镜像进行进程扫描

vol.py -f easy_dump.img --profile=WinSP1x64 pslist

vol.py -f easy_dump.img --profile=WinSP1x64 pstree

vol.py -f easy_dump.img --profile=WinSP1x64 psscan

发现可疑进程notepad.exe，那么我们直接把记事本内容给提取出来。

记事本内容dump

vol.py -f easy_dump.img --profile=Win7SP1x64 memdump -p 2616 -D ./

把记事本内容dump出来，利用string-grep对dmp文件内容进行检索。

记事本内容直接搜索

strings -eb 2616.dmp | grep flag

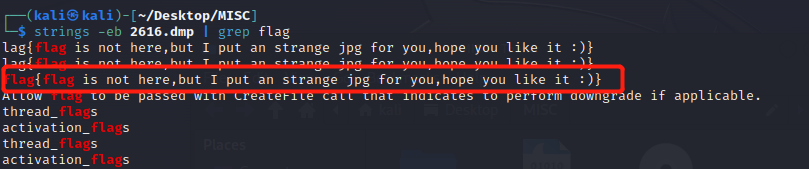
-el 也适用， -u相关用法不太不清楚具体案例，从而得到提示，找jpg文件。

根据提示查找图片并导出

vol.py -f easy_dump.img --profile=Win7SP1x64 filescan | grep .jpg

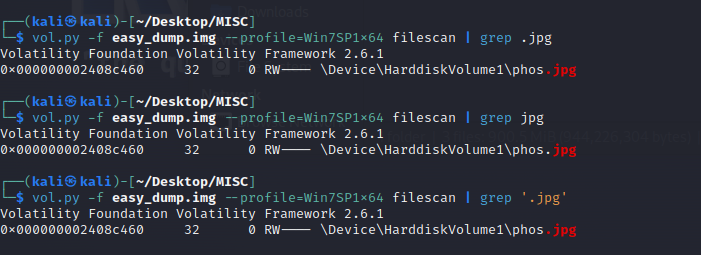
grep进行过滤，也可用其他形式进行检索，主体包含jpg即可。

vol.py -f easy_dump.img --profile=Win7SP1x64 dumpfiles -Q 0x000000002408c460 -D ./

直接导出的就是file:xxxx的格式，我们直接按照需求把文件改成原始文件名即可，eg: phos.jpg

图片隐写分析

有图片就回归到图片方面的隐写分析之上。

binwalk分析，发现存在zip，那么直接对其进行foremost提取。

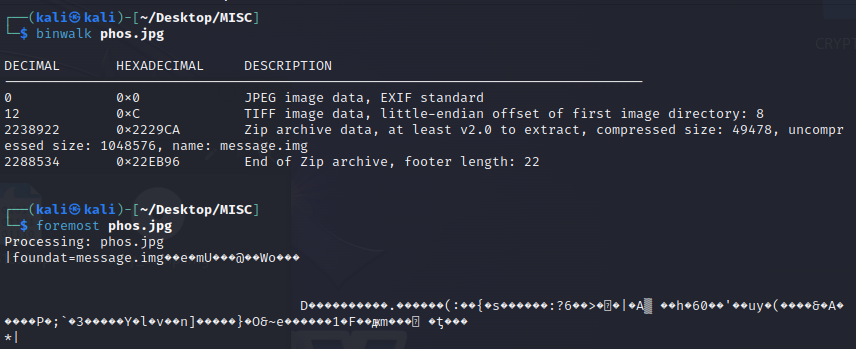
提取出来一个message.img。

再次进行提取操作，本次使用binwalk -e 进行提取hint.txt。

使用foremost无法分离出来hint.txt文件

生成二维码

gnuplot转换

gnuplot         
        G N U P L O T
        Version 5.4 patchlevel 4    last modified 2022-07-10 

        Copyright (C) 1986-1993, 1998, 2004, 2007-2022
        Thomas Williams, Colin Kelley and many others

        gnuplot home:     http://www.gnuplot.info
        faq, bugs, etc:   type "help FAQ"
        immediate help:   type "help"  (plot window: hit 'h')

Terminal type is now 'qt'
gnuplot> plot'hint.txt'
gnuplot>

然后直接输出二维码图片

脚本转换 暂且没成功…… -> 成功了，原终端为agg，无图形界面，需要切换为图形界面显示的终端TkAgg

import matplotlib.pyplot as plt
import matplotlib # keypoint
matplotlib.use('TkAgg') # keypoint
import numpy as np
x = []
y = []
with open('hint.txt', 'r') as f:
    datas = f.readlines()
    for data in datas:
        arr = data.split(' ')
        x.append(int(arr[0]))
        y.append(int(arr[1]))

plt.plot(x, y, 'ks', ms=1)
plt.show()

扫描即可得到信息：1. 维吉尼亚密钥为aeolus 2. 加密后的密文被删除了

恢复镜像删除信息

使用testdisk进行恢复：testdisk message.img，进入相应的操作界面。

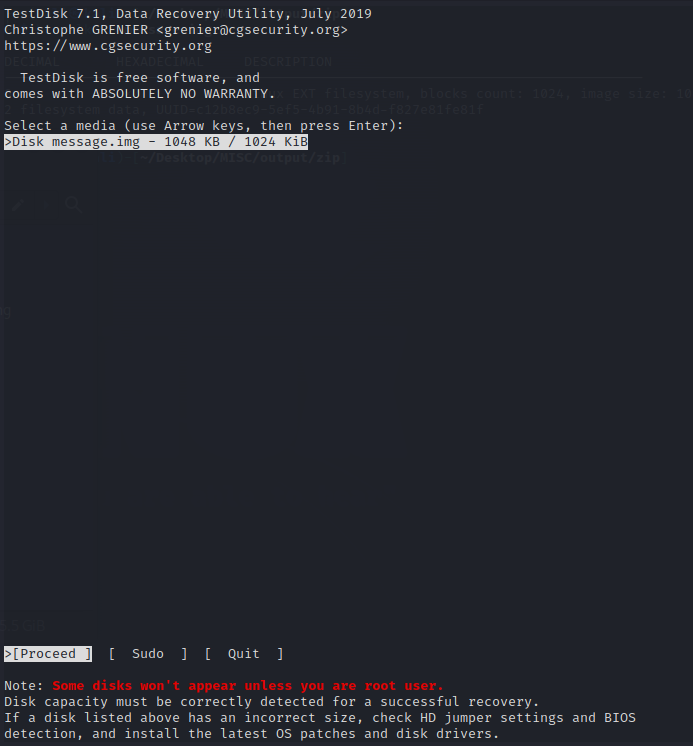
进入Proceed。

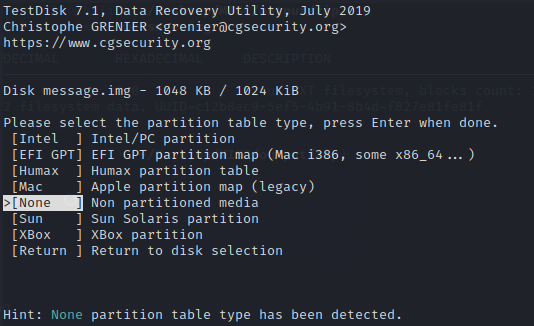
进入None。

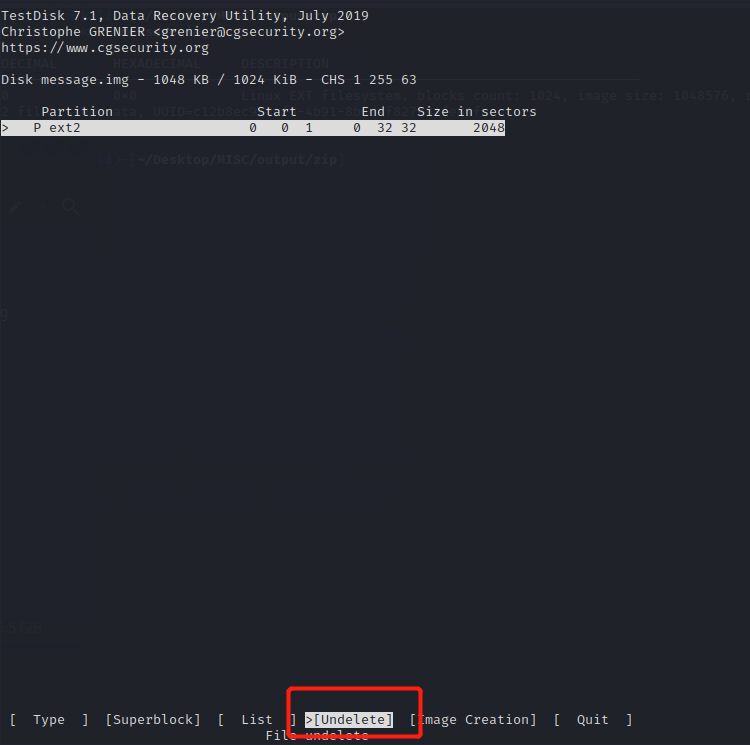
因为涉及删除的文件，所以直接找该功能模块Undelete。

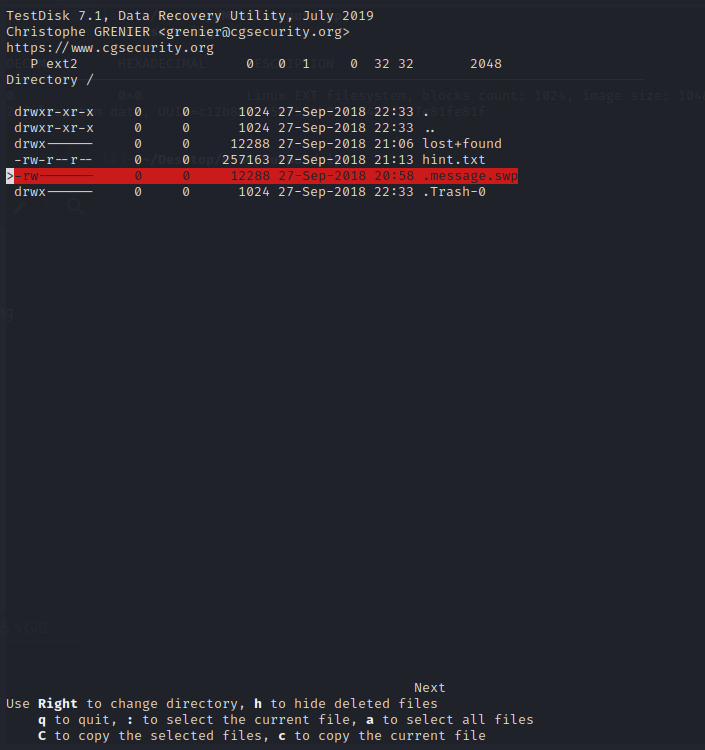
找到标红处，说明该处存在删除文件。

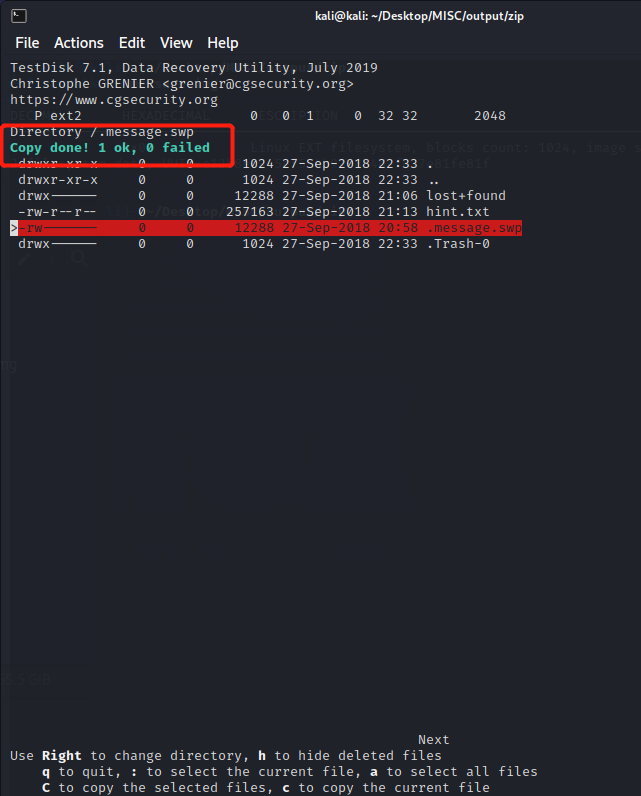
按c确定文件以及路径之后，出现该红框内内容说明导出成功。

到保存路径之下，使用ls -a发现保存下来的文件，直接利用strings查找字符串即可。

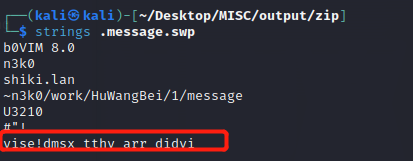
找到加密后的密文，使用在线解密网站结合密钥解密即可，最终得到相应的flag。

230309

strings用法

Usage: strings [option(s)] [file(s)]
 Display printable strings in [file(s)] (stdin by default)
 The options are:
  -a - --all                Scan the entire file, not just the data section [default]
  -d --data                 Only scan the data sections in the file
  -f --print-file-name      Print the name of the file before each string
  -n <number>               Locate & print any sequence of at least <number>
    --bytes=<number>         displayable characters.  (The default is 4).
  -t --radix={o,d,x}        Print the location of the string in base 8, 10 or 16
  -w --include-all-whitespace Include all whitespace as valid string characters
  -o                        An alias for --radix=o
  -T --target=<BFDNAME>     Specify the binary file format
  -e --encoding={s,S,b,l,B,L} Select character size and endianness:
                            s = 7-bit, S = 8-bit, {b,l} = 16-bit, {B,L} = 32-bit
  --unicode={default|show|invalid|hex|escape|highlight}
  -U {d|s|i|x|e|h}          Specify how to treat UTF-8 encoded unicode characters
  -s --output-separator=<string> String used to separate strings in output.
  @<file>                   Read options from <file>
  -h --help                 Display this information
  -v -V --version           Print the program's version number
strings: supported targets: elf64-x86-64 elf32-i386 elf32-iamcu elf32-x86-64 pei-i386 pe-x86-64 pei-x86-64 elf64-little elf64-big elf32-little elf32-big pe-bigobj-x86-64 pe-i386 pdb srec symbolsrec verilog tekhex binary ihex plugin

230310

新讲述视角

关于逆元的作用

Dynamic Programming-DP

贪心算法引论

https://www.zhihu.com/question/23995189/answer/613096905

先来看看生活中经常遇到的事吧——假设您是个土豪，身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w，需要用到尽量少的钞票。

　　依据生活经验，我们显然可以采取这样的策略：能用100的就尽量用100的，否则尽量用50的……依次类推。在这种策略下，666=6×100+1×50+1×10+1×5+1×1，共使用了10张钞票。

　　这种策略称为“贪心”：假设我们面对的局面是“需要凑出w”，贪心策略会尽快让w变得更小。能让w少100就尽量让它少100，这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明，贪心策略是正确的。

但是，如果我们换一组钞票的面值，贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11，那么我们在凑出15的时候，贪心策略会出错：
　　15=1×11+4×1 （贪心策略使用了5张钞票）
　　15=3×5 （正确的策略，只用3张钞票）
　　为什么会这样呢？贪心策略错在了哪里？

鼠目寸光。
　　刚刚已经说过，贪心策略的纲领是：“尽量使接下来面对的w更小”。这样，贪心策略在w=15的局面时，会优先使用11来把w降到4；但是在这个问题中，凑出4的代价是很高的，必须使用4×1。如果使用了5，w会降为10，虽然没有4那么小，但是凑出10只需要两张5元。
　　在这里我们发现，贪心是一种只考虑眼前情况的策略。

我们能这样干，取决于问题的性质：求出f(n)，只需要知道几个更小的f(c)。我们将求解f(c)称作求解f(n)的“子问题”。

　　这就是DP（动态规划，dynamic programming）.

　　将一个问题拆成几个子问题，分别求解这些子问题，即可推断出大问题的解。

基本概念以及DP定义

【无后效性】

　　一旦f(n)确定，“我们如何凑出f(n)”就再也用不着了。

　　要求出f(15)，只需要知道f(14),f(10),f(4)的值，而f(14),f(10),f(4)是如何算出来的，对之后的问题没有影响。

　　“未来与过去无关”，这就是无后效性。

　　（严格定义：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。）

【最优子结构】

　　回顾我们对f(n)的定义：我们记“凑出n所需的最少钞票数量”为f(n).

　　f(n)的定义就已经蕴含了“最优”。利用w=14,10,4的最优解，我们即可算出w=15的最优解。

　　大问题的最优解可以由小问题的最优解推出，这个性质叫做“最优子结构性质”。

　　引入这两个概念之后，我们如何判断一个问题能否使用DP解决呢？

　　能将大问题拆成几个小问题，且满足无后效性、最优子结构性质。

C语言实现快排算法，以及从概念理解算法运行

// 左闭右开
void quickSort(int l, int r) {
    if(l >= r - 1) return;              // 只有单个元素待排序，直接返回

    int flag = a[rand() % (r-l) + l];   // 随机取哨兵
    
    int p = l, q = r;       
    // tmp[l,p): 比 flag 小的；tmp[q, r): 比 flag 大的

    for(int i=l; i<r; i++) {
        if(a[i] < flag)
            tmp[p++] = a[i]; // 比哨兵矮的放在左边
        else if(a[i] > flag)
            tmp[--q] = a[i]; // 比哨兵高的放在右边
    }

    for(int i=p; i<q; i++)   // 与哨兵一样高的
        tmp[i] = flag;

    for(int i=l; i<r; i++)   // 覆盖回 a 数组
        a[i] = tmp[i];
    
    quickSort(l, p);         // 递归
    quickSort(q, r);
}

Kerckhoffs 原则

加密方法不应该被保密，唯一需要保密的是通信双方的 key.
(Kerckhoffs’s principle, 柯克霍夫原则)

柯克霍夫原则要求，一个加密方案的安全性，仅取决于密钥的安全性，而不取决于算法的秘密。接受 Kerckhoffs 原则会带来很多好处：首先，由于加密算法是公开的，通讯各方只需要保密密钥（这显然比加密算法要短，按常理来讲，越短的东西越容易保密）。另外，如果密钥泄露了，双方只需要改个新的密钥就能继续安全通信（若不遵循 Kerckhoffs 原则，一旦泄露算法就需要重新设计加密方案）。最后，遵循 Kerckhoffs 原则可以带来标准化的好处：多人通讯时，可以采用相同的算法而选择不同的密钥，这样程序可以复用。

充分密钥空间原则

任何安全的加密方案，其密钥空间$\mathcal{M}$必须能抵御穷举搜索。
(这一原则在 $|\mathcal{M}|$>$|\mathcal{K}|$ 时有效。若可能的明文比可能的密钥还少，枚举出所有可能的密钥，解密之后会获得比明文空间还大的候选明文集合。)

根据当前计算机的计算能力，密钥空间需要非常大，例如$2^{70}$.

需要注意的是，满足充分密钥空间原则的加密方案，未必就是安全的。

index of coincidence (IoC，重合因子)

IoC方式查找维吉尼亚密钥长度。

流密码

上面介绍的利用 PRG（伪随机发生器）的异或方案，称为流密码。想要执行加密，是先生成一个伪随机的比特流，然后用这个比特流来与明文异或，产生密文。由于流密码方案与生成比特流的方案是绑定的，我们以后直接用“流密码”来简称伪随机比特串发生器。

实际应用中，有 RC4 等流密码方案。RC4 不太安全，LFSR 非常不安全。目前来看，主张采用分组密码来进行加密；如果一定要用流密码，一般用分组密码造一个流出来。

Latex字母显示

希腊字母$\Alpha$
黑板粗体$\mathbb{A}$
正粗体$\mathbf{A}$
斜体数字$\mathit{0123456789}$
罗马体$\mathrm{A}$
哥特体$\mathfrak{A}$
手写体$\mathcal{A}$
希伯来字母$\aleph \beth \gimel \daleth$

230313

准备搭建框架

https://lazzzaro.github.io/2022/12/16/crypto-%E5%90%8E%E9%87%8F%E5%AD%90%E5%AF%86%E7%A0%81/

感觉前置介绍还是有必要的，级别：低级

主体介绍：发展趋势，推广应用

发展趋势：后量子密码，密码学发展历程
推广应用：安全协议，区块链，安全多方计算
发展趋势
- 去信任化
- 隐私数据处理/模糊
- 后量子密码

经典Chameleon Hash构造

下面我们来看一个经典的Chameleon Hash构造。这个构造是2000年提出的，最为直观和经典的Chameleon Hash构造。有兴趣的朋友们可以参看下面的论文。

Krawczyk H, Rabin T. Chameleon hashing and signatures. NDSS 2000: 143-154.

(sk, pk) = KeyGen($\lambda$)。首先，构造一个满足安全常数的循环群G（比如mod p群就可以）。选择一个G群的生成元g，选择一个随机的指数x，计算h = $g^x$。那么，私钥sk = x，公钥pk = (g, h)。
Hm = Hash(pk, m, r)。给定消息m以及一个随机的指数r，Hash的结果为$Hm = g^m h^r$。
r’ = UForge(sk, m, r, m’)。算法简单地根据等式$m + xr = m’ + xr’$来计算$r’$。

我们注意到，因为$m+xr = m’+xr’$成立，因此Hash的结果中有$g^{m} \cdot h^{r} = g^{m} \cdot g^{(xr)} = g^{(m + xr)} = g^{(m’ + xr’)} = g^{m’} \cdot h^{r’}$。伪造成立。

然而，对于其他人来说，其不知道x的值，因此，如果想构造出一个碰撞，其他人必须在指数上面解方程$g^(m + xr) = g^(m’ + xr’)$，也就是说去求一个离散对数问题。但是，离散对数问题直到现在为止都没有一个很快的算法（最快也是指数级的）。因此对于其他人来说，很难找到碰撞。

我们可以看出，这个算法非常的巧妙。利用了离散对数问题求解困难这个事实，构造了一个Chameleon hash。

算法

B+树（IO次数更少；查询性能稳定；范围查询简便）

B-树

230314

paillier cryptosystem

The first pattern：

随机选择两个大质数$p$、$q$满足$gcd(pq, (p-1)*(q-1))$。
计算$n=pq，λ = lcm(p-1, q-1) = (p-1)(q-1) / gcd(p-1,q-1)$
选择随机整数$g$，$0<g<n^2$
定义$L(x) = (x-1) / n$
计算$μ = (L(g^λ \mod n^2 ))^{-1} \mod n$
公钥为$(n，g)$
私钥为$(λ，μ)$

The second pattern（a simpler variant）：

其余参数不变，主要改变了$g$，$λ$，$μ$的定义

随机选择两个大质数$p$、$q$满足$gcd(pq, (p-1)*(q-1))$。
计算$n=pq，λ = lcm(p-1, q-1) = (p-1)(q-1) / gcd(p-1,q-1)$
定义$L(x) = (x-1) / n$
$g = n+1$
$λ = φ(n) = (p-1)*(q-1)$
$μ = φ(n)^{-1} \mod n$

Encryption

设$m$为要加密的消息，显然需要满足，$0 ≤ m ＜ n$
选择随机 $r$，保证$gcd(r, n) = 1$
密文$c$：$c = (g^m) *(r^n) \mod n^2$

Decryption

$m = ( L( c^λ \mod n^2 ) \times μ ) \mod n$

230315

博文-paillier-cryptosystema
paillier-cryptosystem1/2

经过证明之后，发现上证明需要用到一些定理。

paillier1/2涉及定理

费马小定理
欧拉函数

复现-not RSA

mid
200
paillier-2

复现-paillier

mid
200
paillier-2

230316

lru_cache

lru_cache是通过著名的LCU算法来实现的，也就是最近最久未使用缓存淘汰算法。

惊奇

计算器居然有程序员类型的！

amazing！

逆向

x64，实现分配栈空间，然后以分配的栈空间为基准进行数据的存放。

230317

又战旗鼓之整活黑白夜的灰

_config.next.yml新增Darkmode JS
- 修改默认按钮
- pjax默认为true
安装插件

= =, 怎么突然又可以了，神奇！

但代码又有点颜色怪异，稍微修改下代码颜色吧。

230320

Windows安全日志

查看步骤

事件查看器
- 或 eventvwr
Windows日志
- 安全

文件以及格式

.evtx （Win7以后）
.evt （XP，server2003）

日志ID

系统system：

1074，查看计算机的开机、关机、重启的时间以及原因和注释。

6005，表示日志服务已启动，用来判断正常开机进入系统。

6006，表示日志服务已停止，用来判断系统关机。

6009，表示非正常关机， 按ctrl、alt、delete键关机。

41，表示系统在未先正常关机的情况下重新启动。当出现意外断电关机、系统崩溃时，出现此事件ID。

4199，当发生TCP/IP地址冲突的时候，出现此事件ID，用来排查用户IP网络的问题。

35,36,37，记录时间客户端状态信息，35表示更改时间源，36表示时间同步失败，37表示时间同步正常

134，当出现时间同步源DNS解析失败时会出现此事件ID。

7045，服务创建成功

7030，服务创建失败

—————————————————————————————————————————
安全Security

4624，表示成功登陆的用户，用来筛选该系统的用户登陆成功情况。

4625，表示登陆失败的用户，用来判断RDP爆破的情况。

4672，表示授予了特殊权限

4720,4722,4723,4724,4725,4726,4738,4740，事件ID表示当用户帐号发生创建，删除，改变密码时的事件记录。

4727,4737,4739,4762，表示当用户组发生添加、删除时或组内添加成员时生成该事件。

事件日志级别

右侧界面-筛选当前日志
级别
- 关键
- 警告
- 详细
- 错误
- 信息
关键字
- 审核成功
- 审核失败
日志格式
- 头字段
  - 安全日志来源一般不看
- 描述字段
  - 即，详细信息。日志内容更为丰富，分析重点。

本地安全策略

如何把Win7家庭普通版升级成Win7旗舰专业版_百度知道 (baidu.com)

家庭版可能没有
命令行查看secpol.msc
审核策略类别

审核策略	说明
审核账户登录事件	审核任何登录到其他计算机的账户登录与注销事件。
审核账户管理	审核对用户、组、计算机的管理事件。
审核目录服务访问	审核AD环境中设置有系统访问控制列表的AD对象。
审核登录事件	审核用户账户登录与注销事件。
审核对象访问	审核用户账户访问对象的事件。
审核策略更改	审核用户账户的权限分配策略、审核策略以及信任策略更改的事件。
审核特权使用	审核用户执行由“用户权限分配”中制定权限的事件。
审核过程跟踪	审核程序、进程、句柄及对象访问等详细事件。
审核系统事件	审核用户重新启动或关闭计算机、或者对系统安全及安全日志有关的事件。

账户类型
- 域账户：存储在AD中
- 本地账户：存储在本地的SAM文件中
登录事件详解
- 登录会话类型（5）
- 事件类型（9）
  - 右键-看事件属性

登录类型	登录权限	典型情况
本地交互式：使用本地的控制台登录	本地登录	使用域或者本地账户登录本地主机
网络方式：从网络上的某个主机访问windows资源	从网络访问主机	例如访问一台主机的某个共享文件夹
远程交换式：通过远程桌面、终端服务或远程帮助登录某个远程主机	运行通过终端服务登录	使用本地mstsc客户端远程登录某台主机
批作业：用于作为一个指定的账户来运行一个计划任务	作为批作业登录	指定计划任务时指定的以某个具体账户来运行
服务方式：用于以指定的账户来运行某个服务	以服务方式登录	指在指定服务运行时以本地系统账户或者是具体某个账户运行

登录类型	说明
登录类型2	交互式登录（Interactive）
登录类型3	网络（Network）
登录类型4	批处理（Batch）
登录类型5	服务（Service）
登录类型7	解锁（Unlock）
登录类型8	网络明文（NetworkCleartext）
登录类型9	新凭证（NewCredentials）
登录类型10	远程交互（RemoteInteractive）
登录类型11	缓存交互（CachedInteractive）

失败事件
- ID4625
- 查看子ID

子ID	说明
0xC000006A	Anincorrect password was supplied
0xC000006F	Theaccount is not allowed to log on at this time
0xC0000064	Theaccount does not exist
0xC0000070	Theaccount is not allowed to log on from this computer
0xC0000071	Thepassword has expired
0xC0000072	Theaccount is disabled

Linux安全日志

常见日志分类
日志的优先级
message日志
- egrep -ri 'error|warn' /var/log/messages
maillog邮件相关日志
- cat mallog
secure日志
- 记载系统安全信息。最典型的就是登录情况。
- 登录成功与否；账号的增删改情况。
boot.log
- 该日志主要记载系统启动过程
Boot.log
- 该日志主要记载系统启动过程
last.log
- 最近一次成功登陆记录
……

IIS日志分析+Mysql日志分析

跟web整个攻击思路比较类似。

MySQL日志安全分析技巧 - SecPulse.COM | 安全脉搏

访问 /test.php?id=1，此时我们得到这样的日志：

190604 14:46:14       14 Connect    root@localhost on
                      14 Init DB    test   
                      14 Query    SELECT * FROM admin WHERE id = 1     
                      14 Quit

第一列：Time，时间列，前面一个是日期,后面一个是小时和分钟，有一些不显示的原因是因为这些sql语句几乎是同时执行的,所以就不另外记录时间了。
第二列：Id，就是show processlist出来的第一列的线程ID,对于长连接和一些比较耗时的sql语句,你可以精确找出究竟是那一条那一个线程在运行。
第三列：Command，操作类型，比如Connect就是连接数据库，Query就是查询数据库(增删查改都显示为查询)，可以特定过虑一些操作。
第四列：Argument，详细信息，例如 Connect root@localhost on 意思就是连接数据库，如此类推,接下面的连上数据库之后,做了什么查询的操作。

MySQL中的log记录是这样子：

Time                 Id        Command         Argument
190601 22:03:20     98 Connect  root@192.168.204.1 on
        98 Connect  Access denied for user 'root'@'192.168.204.1' (using password: YES)      
        103 Connect  mysql@192.168.204.1 on       
        103 Connect  Access denied for user 'mysql'@'192.168.204.1' (using password: YES)      
        104 Connect  mysql@192.168.204.1 on       
        104 Connect  Access denied for user 'mysql'@'192.168.204.1' (using password: YES)      
        100 Connect  root@192.168.204.1 on       
        101 Connect  root@192.168.204.1 on       
        101 Connect  Access denied for user 'root'@'192.168.204.1' (using password: YES)       
        99 Connect  root@192.168.204.1 on        
        99 Connect  Access denied for user 'root'@'192.168.204.1' (using password: YES)      
        105 Connect  mysql@192.168.204.1 on       
        105 Connect  Access denied for user 'mysql'@'192.168.204.1' (using password: YES)      
        100 Query  set autocommit=0      
        102 Connect  mysql@192.168.204.1 on       
        102 Connect  Access denied for user 'mysql'@'192.168.204.1' (using password: YES)      
        100 Quit

利用爆破工具，一个口令猜解成功的记录是这样子的：

1
2
3

190601 22:03:20     100 Connectroot@192.168.204.1 on
   100 Queryset autocommit=0   
   100 Quit

其他方式登录成功的记录：

# Navicat for MySQL登录：
190601 22:14:07  106 Connectroot@192.168.204.1 on         
         106 QuerySET NAMES utf8
         106 QuerySHOW VARIABLES LIKE 'lower_case_%'         
         106 QuerySHOW VARIABLES LIKE 'profiling'         
         106 QuerySHOW DATABASES

# 命令行登录
190601 22:17:25  111 Connectroot@localhost on
         111 Queryselect @@version_comment limit 1
         190601 22:17:56  111 Quit

登录失败的记录：

1 2	102 Connect mysql@192.168.204.1 on 102 Connect Access denied for user 'mysql'@'192.168.204.1' (using password: YES)

230321

日志分析题目流程

Windows日志分析

关键字3389 -> 远程连接 -> 登录类型 10
先筛选529失败的
再筛选528成功的
两者结合查看，查找到登录IP192.168.152.1以及初次登录时间为2015/10/21 16:11:34

Linux日志分析

利用notepad++，进行标记以及过滤
- 标记
- 同时标记所在行
- 搜索 -> 删除未标记行
关键字failed 、accepted进行综合分析
192.168.4.23
Nov 19 17:28:47

230323

复现-日志分析

均用notepad++

IIS日志分析

大概看过一遍所给文件
中间存在admin，先把相关条目过滤出来
再看下大概，发现存在大量404，利用200过滤出来
可以直接利用正则匹配admin.*200过滤

sql日志分析

布尔盲注

先过滤出flag_is_here关键字
再过滤出响应码为200的数据
可以看出是布尔盲注
可以直接看出具体的数值 flag_list = [102, 108, 97, 103, 123, 115, 113, 108, 109, 48, 112, 95, 53, 49, 95, 112, 48, 119, 101, 114, 102, 117, 108, 125]，写脚本稍微转换可得flag{sqlm0p_51_p0werful}
写脚本提取转换

import re

f = open('access.log', 'r')
lines = f.readlines()
datas = []

flag_dic = {}
for line in lines:
    matchObj = re.search(r'LIMIT 0,1\),(.*?),1\)\)>(.*?) AND', line)
    if matchObj:
        flag = int(matchObj.group(1))
        value = int(matchObj.group(2)) + 1
        flag_dic[flag] = value
    print(flag_dic)
flag = ''
for value in flag_dic.values():
    flag += chr(value)
print(flag)

sql时间盲注

用工具进行url-decode
利用sleep(3)继续过滤，最后得到符合条件的数据
观察发现，里面时间相同的可能为flag
写脚本进行提取

import re

f = open('sql', 'r')
lines = f.readlines()
flag = ''
# print(lines[0])
# 正则匹配得到相关数据
for i in range(len(lines)):
    try:
        f1 = re.search(r'(\d+:\d+:\d+) -0500] \"GET /web/admin/sql.php\?id=-1 union select 1,IF\(MID\(\(select f1ag from f1ag limit 0,1\),\d+,1\)\=binary\(\'(.*?)\'\)', lines[i-1])
        f2 = re.search(r'(\d+:\d+:\d+) -0500] \"GET /web/admin/sql.php\?id=-1 union select 1,IF\(MID\(\(select f1ag from f1ag limit 0,1\),\d+,1\)\=binary\(\'(.*?)\'\)', lines[i])
        # print(f1)
        if f1[1] == f2[1]:
            print(f1[1])
            flag += f1[2]
    except:
        continue
print(flag)

字典

字典设置键值之后可以不停替换value

适合直接键值固定但value不固定的盲注。

230327

x=pow(m,p,n)
y=pow(m,q,n)
x=m^p%n 一
y=m^q%n 二

x=m^p%n
两边同时平方个q
x^q=(m^p)^q%n
x^q=m^n%n
x^q=(m^q)^p%n
x^q=(m^q%n)^p%n
将式 二代入
x^q=y^p%n
两边同时平方个p
(x^q)^p=(y^p)^p%n
x^(q*p)=(y^p)^p%n
x^n=(y^p)^p%n

x^n=(y^p)^p+kn
x^n=(y^p)^p+kpq
#两边同时模p
x^n%p=(y^p)^p%p+kpq%p
x^n%p=(y^p)^p%p
#根据费马小定理
a^p-1%p=1 a^p%p=a
x^n%p=(y^p)%p
x^n%p=y%p
x^n=y+kp
x^n-y=kp
kp=x^n-y
利用公约数求p
p=gcd(x^n-y,n)

230404

黄金分割查找法

fib = lambda n: n if n < 2 else fib(n-1) + fib(n-2)
def fib_search(arr, x):
    left = 0
    right = len(arr) - 1

    key = 0
    while fib(key) < len(arr):
        key += 1

    while left <= right:
        mid = min(left + fib(key - 1), len(arr) - 1)
        if x < arr[mid]:
            right = mid - 1
            key -= 1
        elif x > arr[mid]:
            left = mid + 1
            key -= 2
        else:
            return mid
    return 0


fib_list = [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
flag_list = [1, 2, 8, 1, 0, 1, 3, 3, 5, 8, 2, 3, 0, 5, 2, 3, 2, 1, 0, 1, 13, 9, 7, 12, 8, 4, 2, 7, 9, 11, 1, 5]

flag = ''
for i in flag_list:
    flag += str(fib_search(fib_list, x=i))
# assert len(flag) == 32
print('flag{' + flag + '}')
# arr为使用的斐波那契数列
# x为使用的查询密钥

230406

哈希查找法

$$
H = f(key)
$$

哈希表存储位置主要由key来确定

具体的介绍主要看OneNote-2023-04-04

构建哈希表
1. 直接定址法
2. 数字分析法
3. 平方取中法
4. 折叠法
  1. 移位折叠
  2. 间界折叠
5. 除留余数法
6. 随机数法
处理冲突
1. 开放定址法
  1. 线性探测法
  2. 二次探测法
  3. 伪随机数探测法
2. 再哈希法
3. 链地址法
4. 建立公共溢出区

分块查找法

索引查找法

类似数据库中的索引查找，算法核心依旧是线性查找。

进行分块
1. 分块数目自定
2. 块内无序，块外有序，整体升序或者降序
3. 前一块的max，必须小于后一块的min
建立索引表

临时换源

https://pypi.tuna.tsinghua.edu.cn/simple #清华
https://pypi.mirrors.ustc.edu.cn/simple/ #中国科技大学
https://mirrors.aliyun.com/pypi/simple/ #阿里
http://pypi.douban.com/simple/ #豆瓣

230407

存在zsh_history报错

zsh: corrupt history file ~/.zsh_history

存在上述报错，基本因为关机的时候啥都没退，导致中断保存，再开启时就出现如上报错信息。

上网查找报错信息有各种方法，但当前选择了最简单直接的方法，就直接暴力删除原始文件。

1	rm /home/kali/.zsh_history

230331

密钥爆破 <- 伪加密 <- 掩码爆破

掩码爆破

已知密码是这串字符，你知道如何爆破出来嘛？

提示：都是小写字母。

do_u_like_xxx

230411

vscode运行sagemath

vscode+jupyternotebook+sagemath配置 - 知乎 (zhihu.com)

主要原理就是直接利用sagemath自带的notebook（jupyter）的server运行代码。

红框内直接打开运行。

运行得到本地地址 + token的形式，我们主要利用这样一串字符串进行调用。

打开vsCode，前置准备比如vscode配置python啥的，修改代码颜色啥的就不提了。

直接到切换configuration一步。

SageMath 9.3为我们调用服务器之后出现的配置。

选择Select，选择Existing选项。把上面一串带token的字符串直接输入，然后等待连接，即可完成配置，重启一下，即可在vscode中使用sagemath。

新建文件后缀名为.ipynb，然后就可以按照像sagemath-notebook一样进行操作，使用python的代码颜色，能够直接像pycharm一样识别一些函数，但有时候又不会显示。

总体来说，比最原始的shell以及notebook，要更为方便一点。

我很满意，甚至想把pycharm也给换了，用vscode运行python代码。不过先继续尝试吧，找到合适的使用方法。

230412

一些数学概念

平凡

平凡就是指最简单的情形，或者说是容易证明的、容易看到的。

非平凡

非零解？

退化

“退化”的话，在数学里面有“不可逆”、“不满秩”这样的含义。它一般跟“某个量等于0”有关。

pwntools的使用

context模块使用

context.clear()	        ## 清除当前运行时变量
context.arch = ‘arm’	## 设置架构：amd64、i386、arm、mips
context.os = ‘linux’	## 设置操作系统：linux
context.bits=‘32’	    ## 设置 32 位或 64 位：32、64
context.endian=‘little’	## 设置字节序：little、big
context.update(os=‘linux’, arch=‘amd64’, bits=64) ## 更新当前运行时变量
context.log_level=‘debug’	                      ## 设置日志级别：debug、info
context.log_file=‘/tmp/pwnlog.txt’	              ## 设置日志保存文件

tube模块使用

- 常用命令
## 连接
  remote('ip',端口)：远程
  process()：本地
## 发送
  send(data) : 发送数据
  sendline(data) : 发送一行数据，相当于在数据末尾加\n
  sendafter(xxx,data)：接收到 xxx 之后发送 data
## 接收
  recv(numb=4096, timeout=default) : 接收指定字节
  recvline(keepends=True) : 接收一行，keepends为是否保留行尾的\n
  recvuntil(delims, drop=False) : 一直读到 delims 的 pattern 出现为止
  recvrepeat(timeout=default) : 持续接受直到EOF或timeout
## 交互
  interactive()  直接进行交互，相当于回到shell的模式，在取得shell之后使用

模块中其他函数

interactive()	  ## 交互模式，能够同时读写管道，通常在获得 shell 之后调用
recv(numb=1096, timeout=default)  ## 接受最多 numb 字节的数据
recvn(numb, timeout=default)	  ## 接受 numb 字节的数据
recvall()	                      ## 接受数据直到 EOF
recvline(keepends=True)	          ## 接受一行，可选择是否保留行尾的 ‘\n’
recvrepeat(timeout=default)	      ## 接受数据直到 EOF 或 timeout
recvuntil(delims,timeout=default) ## 接受数据直到 delims 出现
send(data)	      ## 发送数据
sendafter(delim, data, timeout=default)	 ## 相当于 recvuntil(delim, timeout) 和 send(data) 的组合
sendline(data)	  ## 发送一行，默认在行尾加 “\n”
sendlineafter(delim, data, timeout=default)	## 相当于 recvuntil(delim, timeout) 和 sendline(data) 的组合
close()	          ## 关闭管道

230413

读论文。

一点疑问

p % (q - 1) ==? p - q + 1

from Crypto.Util.number import *
p = getPrime(512)
q = getPrime(512)
assert p > q
test1 = p % (q-1)
test2 = p - q + 1
print(test1)
print(test2)

不太理解。

230417

Lattice

定义格空间，通常情况下$\mathbb{Z}^{n}$，数学定义下是$\mod n$，关键基向量，且可变。
- 初始向量是基向量的定义源？
多项式时间？
覆盖半径，无穷大时存在高斯分布-调和分析
上下界
- 凸体理论

线性相关/线性无关性质

230419

谍影重重

题目是一开始就上线了的，所以当时看到那份 config.json 就猜到了这是要做 vmess 的流量解析，于是翻出来了万恶的 vmess 文档，依照文档开始写解析脚本。

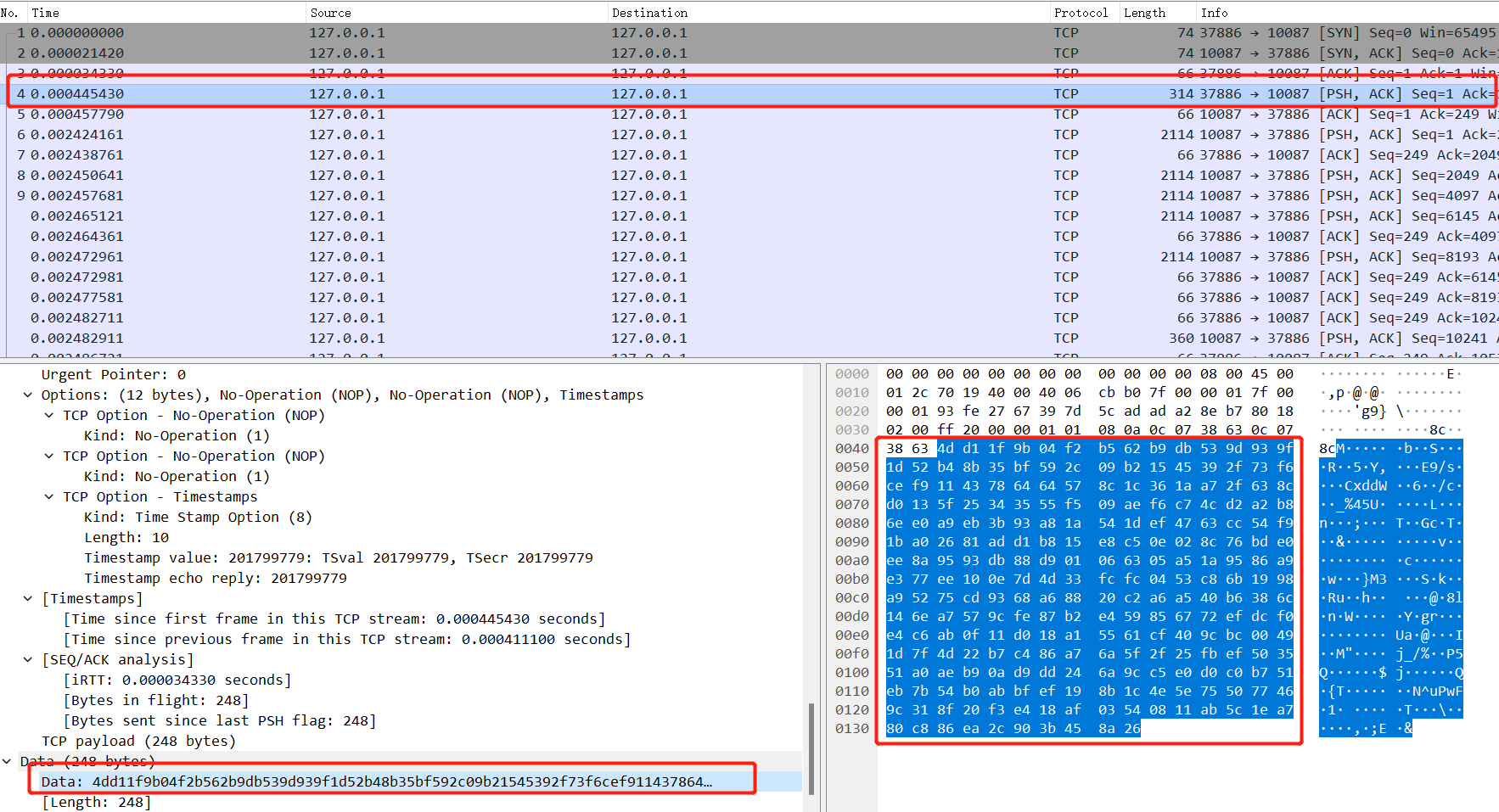
req的相关数据在这一流当中显示。

认证交互的数据在Data部分，直接复制它的值即可。

前16字节是认证哈希值。后面的数据应该就是实际数据？

时间Mar 12, 2021 14:02:42.667325408 中国标准时间

时间戳1615528962.667325408

利用数据包中的时间转换时间戳。

HMAC必须按照特定顺序输入需要的数值才可以。

1	vmess_hmac = lambda x: hmac.new(client_id, x, hashlib.md5).hexdigest()

p(64)一直没办法调用，仔细思考应该是库名冲突了。pwntools的调用是from pwn import *，而之前又安装了不知名的pwn库，所以导致调用冲突吧。

官方文档没更新，看源码3应该是AES-128-GCM

vmess协议

协议细节 - VMess 协议 - 《Project V（V2RAY）文档手册》 - 书栈网 · BookStack

指令部分

指令部分经过 AES-128-CFB 加密：

Key：MD5(用户 ID + []byte(‘c48619fe-8f02-49e0-b9e9-edf763e17e21’))
IV：MD5(X + X + X + X)，X = []byte(认证信息生成的时间) (8 字节, Big Endian)

更新pycharm中的第三方库

右边出现尖角说明可以更新，直接点击进行相关界面，然后勾选安装特定版本即可安装到新版。

如果最新版本是测试版本的话，可以选其他版本。

AES-128-GCM

GCM（ Galois/Counter Mode )
GCM中的G就是指GMAC，C就是指CTR。
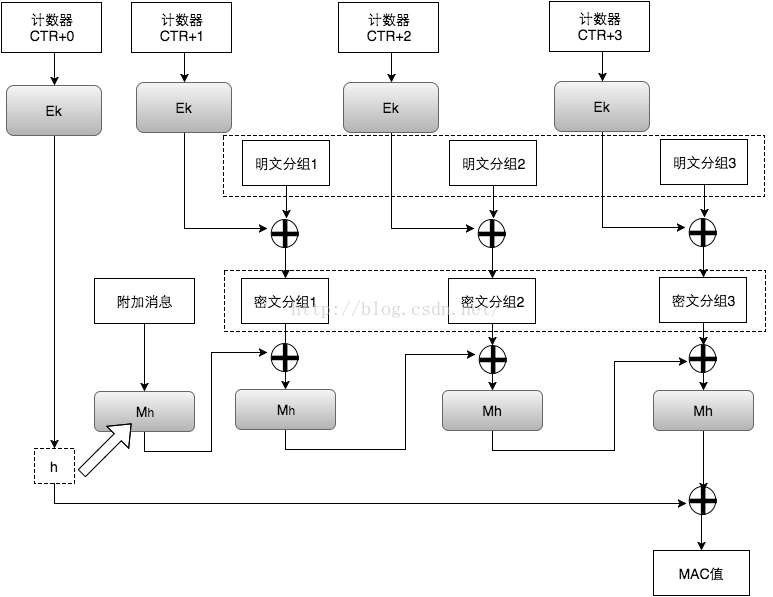
GCM可以提供对消息的加密和完整性校验，另外，它还可以提供附加消息的完整性校验。在实际应用场景中，有些信息是我们不需要保密，但信息的接收者需要确认它的真实性的，例如源IP，源端口，目的IP，IV，等等。因此，我们可以将这一部分作为附加消息加入到MAC值的计算当中。下图的Ek表示用对称秘钥k对输入做AES运算。最后，密文接收者会收到密文、IV（计数器CTR的初始值）、MAC值。

230421

继续整活谍影重重

Malware analysis extracted_at_0x22a7b.exe Malicious activity | ANY.RUN - Malware Sandbox Online

9月26日，Proofpoint研究人员发现一起针对美国接收者的上万的垃圾邮件攻击活动。邮件使用eFax诱饵文件（图1）和URL链接来下载含有恶意宏的文档（图2）。如果用户启用了宏，宏文件就会执行嵌入的Hancitor恶意软件，恶意软件执行后会接收任务来下载两个版本的Pony窃取器和DanaBot银行木马。

病毒分析

Malware analysis extracted_at_0x22a7b.exe Malicious activity | ANY.RUN - Malware Sandbox Online

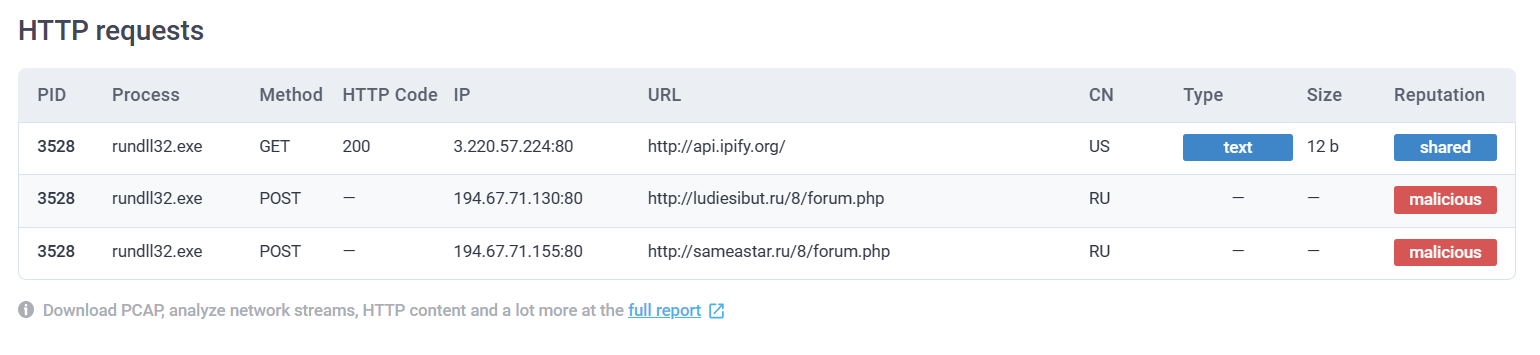
得到url = http://api.ipify.org

题目中所给的压缩包。

根据提示md5一下，得到08229f4052dde89671134f1784bed2d6

得到的文件使用WINHEX打开一下，发现提示了文件类型，是Gob文件

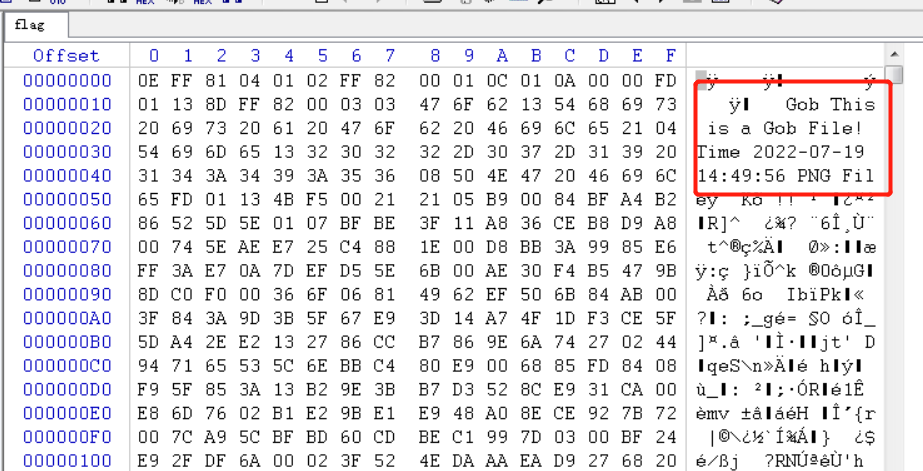
利用属性来进行定义，从而反序列化。

导包的时候出现了missing path，找了报错原因，没解决，后来发现是因为格式错了。

import (
	"fmt"
	"math/rand"
	"time"
	"os"
)

搞出一张图片了，但没明白为啥图片的大小就是70450bytes，有点迷惑。

没找到合适的工具提取隐写，十有八九是提取像素点的。

最终exp

"""
@Author  :Eurynome
@Date    :2023/4/19 17:19
"""
"""
config.json
"settings": {
                "clients": [
                    {
                        "id": "b831381d-6324-4d53-ad4f-8cda48b30811"
                    }
                ]
}
"""

"""
1111
"""
import hmac
import uuid
from pwn import *


client_id = uuid.UUID('b831381d-6324-4d53-ad4f-8cda48b30811').bytes

md5 = lambda x: hashlib.md5(x).hexdigest()
vmess_hmac = lambda x: hmac.new(client_id, x, hashlib.md5).hexdigest()


"""
4dd11f9b04f2b562b9db539d939f1d52 b48b35bf592c09b21545392f73f6cef91143786464578c1c361aa72f638cd0135f25343555f509aef6c74cd2a2b86ee0a9eb3b93a81a541def4763cc54f91ba02681add1b815e8c50e028c76bde0ee8a9593db88d901066305a51a9586a9e377ee100e7d4d33fcfc0453c86b1998a95275cd9368a68820c2a6a540b6386c146ea7579cfe87b2e459856772efdcf0e4c6ab0f11d018a15561cf409cbc00491d7f4d22b7c486a76a5f2f25fbef503551a0aeb90ad9dd246a9cc5e0d0c0b751eb7b54b0abbfef198b1c4e5e755077469c318f20f3e418af03540811ab5c1ea780c886ea2c903b458a26
"""
req = bytes.fromhex('4dd11f9b04f2b562b9db539d939f1d52' + 'b48b35bf592c09b21545392f73f6cef91143786464578c1c361aa72f638cd0135f25343555f509aef6c74cd2a2b86ee0a9eb3b93a81a541def4763cc54f91ba02681add1b815e8c50e028c76bde0ee8a9593db88d901066305a51a9586a9e377ee100e7d4d33fcfc0453c86b1998a95275cd9368a68820c2a6a540b6386c146ea7579cfe87b2e459856772efdcf0e4c6ab0f11d018a15561cf409cbc00491d7f4d22b7c486a76a5f2f25fbef503551a0aeb90ad9dd246a9cc5e0d0c0b751eb7b54b0abbfef198b1c4e5e755077469c318f20f3e418af03540811ab5c1ea780c886ea2c903b458a26')
# print(req)
cut_time = 1615528962
target_hash = req[:16].hex()
# print(target_hash)

def get_cmd_iv(time, target_hash):
    for t in range(time - 50, time + 50):
        cur_hash = vmess_hmac(p64(t))
        # print(t)
        # print(cur_hash)
        if t == 1615528982:
            print(f'time     = {t}')
            return md5(p64(t, endian='big') * 4)

cmd_key = md5(client_id + b'c48619fe-8f02-49e0-b9e9-edf763e17e21')
cmd_iv = get_cmd_iv(cut_time, target_hash)
# print(type(cmd_iv))
# print(type(cmd_key))

print(f"cmd_key  = {cmd_key}")
print(f"cmd_iv   = {cmd_iv}")

# time     = 1615528982
# cmd_key  = "b50d916ac0cec067981af8e5f38a758f"
# cmd_iv   = "881eb47d4d3b67b24328c5178c0eedcc"
print('------------------------------------------------')
"""
2222
"""
from fnvhash import fnv1a_32
from Crypto.Cipher import AES
from Crypto.Util.number import *
cmd_aes = lambda: AES.new(bytes.fromhex(cmd_key), AES.MODE_CFB, bytes.fromhex(cmd_iv), segment_size=128)

cmd = req[16:]
ret = cmd_aes().decrypt(cmd)
# ret = bytes.fromhex('0113277f5732da52ada790d87b8829daa95e4a9aa9ba58c7e3ad36fe2499dca259a20d6300011388017f0000011ace7d9bb0b539182c0381aa405d112d5d1dc1d33ec58e446b151f3331cd5209d25d1b065fa8754486e571584c46fa7d0ee443eb69abf466c28349e9020923cc8f472f1d20bbe05687b720e2cc8fab4dc173c232d6c815cb7c75c6bd74d2e2a57638effd11ff009c36384c431b123ed124965e218a79cfb91155fc55b81faf716aefb58328f295e76e352d11e90317ae8d209038ae70d19ee2f577c4841d77dc426431088a943244f50af3a2ffdf45b8ff210b2c4ff551076127fa')
print(f"ver      = {ret[0:1].hex()}")
print(f"dat_iv   = {ret[1:17].hex()}")
print(f"dat_key  = {ret[17:33].hex()}")
print(f"v        = {ret[33:34].hex()}")
print(f"opt      = {ret[34]:b}")
print(f"p        = {ret[35:36].hex()[0]}")
print(f"sec      = {ret[35:36].hex()[1]}")
p = int(ret[35:36].hex()[0], 16)
print()
print(f"cmd      = {ret[37:38].hex()}")
print(f"port     = {bytes_to_long(ret[38:40])}")
print(f"type     = {ret[40:41].hex()}") #ipv4
print()
print(f"host     = {'.'.join(str(i) for i in ret[41:45])}")
print(f"rand     = {ret[45:45 + p].hex()}")
print(f"F        = 0x{ret[45 + p:45 + p + 4].hex()}")

print(f"check    = {hex(fnv1a_32(ret[:45 + p]))}")

"""
3333
"""
from Crypto.Hash import SHAKE128
class SizeParser:
    def __init__(self, nonce):
        self.shake = SHAKE128.new(nonce)

    def next(self):
        return bytes_to_long(self.shake.read(2))

    def enc(self, size):
        return self.next() ^ size

    def dec(self, size):
        return self.next() ^ size

    def next_padding(self):
        return self.next() % 64

print('------------------------------------------------')

def decrypt(arr, key, iv):
    count = 0
    parser = SizeParser(iv)
    output = []
    print(f"dat_iv   = {key.hex()}")
    print(f"dat_key  = {iv.hex()}")
    while len(arr) > 0:
        padding = parser.next_padding()
        L = parser.dec(bytes_to_long(arr[:2])) - padding

        arr = arr[2:]
        e_iv = p64(count, endian='big')[6:] + iv[2:12]

        try:
            dec = AES.new(key, AES.MODE_GCM, e_iv).decrypt_and_verify(arr[:L-16], arr[L-16:L])
            output.append(dec)
        except:
            print('[!] Decryption failed!')
        finally:
            count += 1
            arr = arr[L + padding:]
    return output


data = cmd[45 + p + 4:]
data_iv = ret[1:17]
data_key = ret[17:33]
# print(type(data_key))
pprint(decrypt(data, data_key, data_iv)[0].decode().split('\r\n'))

"""
4444
"""
print('------------------------------------------------')
res = open('res.bytes', 'rb').read()
# print(res)
res_key = md5(data_key)
res_iv = md5(data_iv)
# print(res_key)
# print(res_iv)
print(f"res_key  = {res_key}")
print(f"res_iv   = {res_iv}")
res_aes = lambda: AES.new(bytes.fromhex(res_key), AES.MODE_CFB, bytes.fromhex(res_iv), segment_size=128)
dec_res = res_aes().decrypt(res[:16])
print(f"v        = {dec_res[0:1].hex()}")
print(f"opt      = {dec_res[1:2].hex()}")
print(f"cmd      = {dec_res[2:3].hex()}")
print(f"c_l      = {dec_res[3:4].hex()}")
cmd_len = int(dec_res[3:4].hex(), 16)
print(f"cmd      = {dec_res[4:4+cmd_len].hex()}")
data = res[4 + cmd_len:]
plaintext = decrypt(data, bytes.fromhex(res_key), bytes.fromhex(res_iv))

"""
5555
"""
# from base64 import b64decode
# data = ''.join(i.decode() for i in plaintext)
# start = data.find("atob('") + len("atob('")
# end = data.find("');", start)
#
# binary = b64decode(data[start:end])
# check_sum = hashlib.sha256(binary).hexdigest()
#
# open('doc.zip', 'wb').write(binary)
print('------------------------------------------------')
from base64 import b64decode

data = "".join(i.decode() for i in plaintext)

start = data.find("atob('") + len("atob('")
end = data.find("');", start)

binary = b64decode(data[start:end])
check_sum = hashlib.sha256(binary).hexdigest()

# open("doc.zip", "wb").write(binary)
print(check_sum)

"""
6666
"""
print('------------------------------------------------')
print(md5(b"api.ipify.org"))

"""
7777
"""
print('------------------------------------------------')
from PIL import Image
import numpy as np
img = Image.open('flag.png')
arr = np.array(img)

ans = bytes(arr[:, :, 3].reshape(2000 * 973)).replace(b'\xff', b'').replace(b'\x00', b'').decode()[:42]
print(ans)
# flag{898161df-fabf-4757-82b6-ffe407c69475}

# from PIL import Image
# pic = Image.open('flag.png')
# w, h = pic.size
# flag = []
# for i in range(h):
#     for j in range(w):
#         piexl = list(pic.getpixel((j, i)))[3]
#         if(piexl != 0xff):
#             flag.append(chr(int(piexl)))
#             if len(flag) == 42:
#                 print(''.join(flag))

# output
time     = 1615528982
cmd_key  = b50d916ac0cec067981af8e5f38a758f
cmd_iv   = 881eb47d4d3b67b24328c5178c0eedcc
------------------------------------------------
ver      = 01
dat_iv   = 13277f5732da52ada790d87b8829daa9
dat_key  = 5e4a9aa9ba58c7e3ad36fe2499dca259
v        = a2
opt      = 1101
p        = 6
sec      = 3

cmd      = 01
port     = 5000
type     = 01

host     = 127.0.0.1
rand     = 1ace7d9bb0b5
F        = 0x39182c03
check    = 0x39182c03
------------------------------------------------
dat_iv   = 5e4a9aa9ba58c7e3ad36fe2499dca259
dat_key  = 13277f5732da52ada790d87b8829daa9
['GET /out HTTP/1.1',
 'Host: 127.0.0.1:5000',
 'User-Agent: curl/7.75.0',
 'Accept: */*',
 'Connection: close',
 '',
 '']
------------------------------------------------
res_key  = b22984cda4143a919b5b6de8121b6159
res_iv   = fa2a8ab0fadb4854943df690335a99b5
v        = a2
opt      = 00
cmd      = 00
c_l      = 00
cmd      = 
dat_iv   = b22984cda4143a919b5b6de8121b6159
dat_key  = fa2a8ab0fadb4854943df690335a99b5
------------------------------------------------
3a5648f7de99c4f87331c36983fc8adcd667743569a19c8dafdd5e8a33de154d
------------------------------------------------
08229f4052dde89671134f1784bed2d6
------------------------------------------------
flag{898161df-fabf-4757-82b6-ffe407c69475}

package main

import (
	"math/rand"
	"os"
	"time"
)

func main() {
	//seed init
	loc, _ := time.LoadLocation("Local")
	timeObj, _ := time.ParseInLocation(
		"2006-01-02 15:04:05",
		"2022-07-19 14:49:56", loc)
	seed := timeObj.Unix()
	rand.Seed(seed)

	input, _ := os.Open("./src.png")
	in := make([]byte, 70475)
	lenx, _ := input.Read(in)
	table := make([]int, lenx)
	out := make([]byte, lenx)
	for i := 0; i < lenx; i++ {
		table[i] = i
	}

	//shuffle
	rand.Shuffle(len(table), func(i, j int) {
		table[i], table[j] = table[j], table[i]
	})

	for i := 0; i < lenx; i++ {
		out[table[i]] = in[i]
	}
	output, _ := os.Create("./flag.png")
	output.Write(out)

}

vscode安装配置golang环境

安装go

官网下载，但应该需要科学，找了个中文网进行下载了。Go下载 - Go语言中文网 - Golang中文社区 (studygolang.com)
直接一路Next下载，最终安装在C盘了。
命令行输入go version，输出如下即表示安装成功。

vs配置go环境

为保证环境能够正常安装下载go插件，需要执行两条命令。

1 2	go env -w GO111MODULE=on go env -w GOPROXY=https://goproxy.cn,direct

验证一下，使用命令go env。

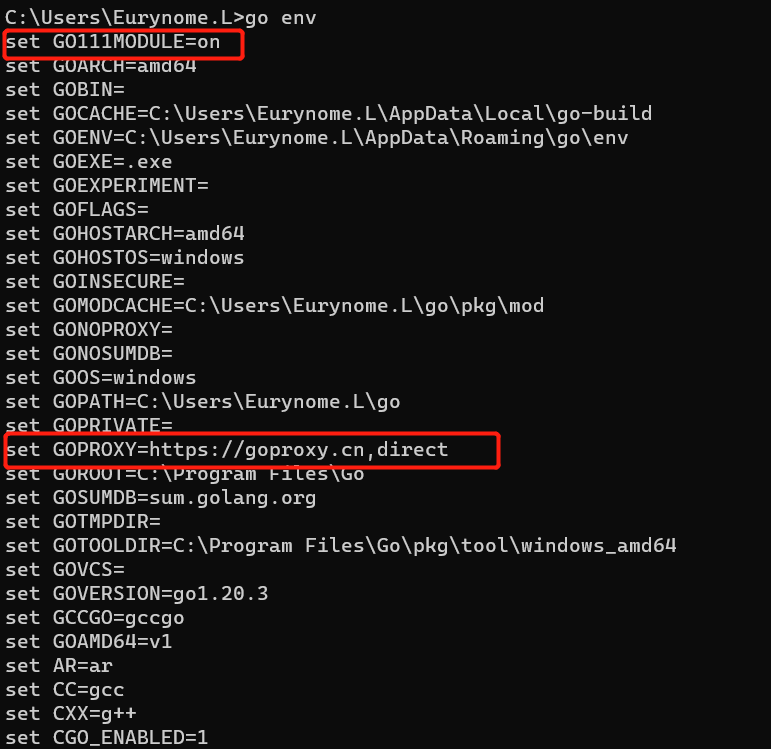
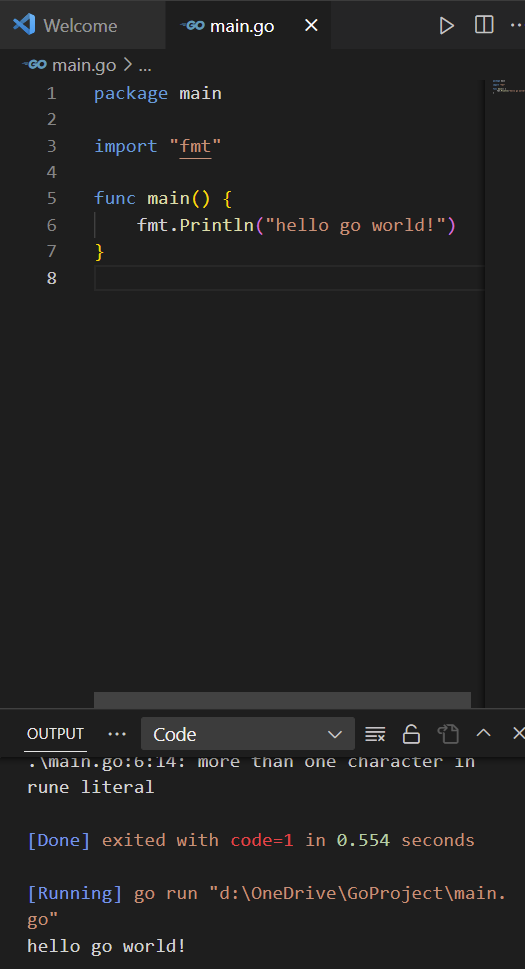
无语，最终测试成功了，写的测试代码一直失败，不知道问题出现在哪里了。

后来发现，行吧，单引号跟双引号在go环境中严格区分。

而且运行代码之前一定要保存文件，要不然胡直接报错。

package main

import "fmt"

func main() {
	fmt.Println("hello go world!")
}

230424

1 2	graph LR w --- x --- y --- z

gantt
        dateFormat  YYYY-MM-DD

        title 软件开发甘特图

        section 设计
        需求:done,des1, 2019-01-06,2019-01-08
        原型:active,des2, 2019-01-09, 3d
        UI设计:des3, after des2, 5d
        未来任务:des4, after des3, 5d

        section 开发
        学习准备理解需求:crit, done, 2019-01-06,24h
        设计框架:crit, done, after des2, 2d
        开发:crit, active, 3d
        未来任务:crit, 5d
        休息时间:2d

        section 测试
        功能测试:active, a1, after des3, 3d
        压力测试:after a1, 20h
        测试报告: 48h

Ethernaut

Function Selector and Argument Encoding - CTF Wiki (ctf-wiki.org)

安装MetaMask

谷歌下载插件，容易因为后台更新导致直接把安装的插件给清除，因为默认安装的插件都是不安全的。
于是跑去火狐下载插件了，火狐浏览器版本问题导致无法验证插件压缩包的签名，无法安装。但火狐能够浏览器内下载插件，现在勉强还是能用。

打开浏览器console

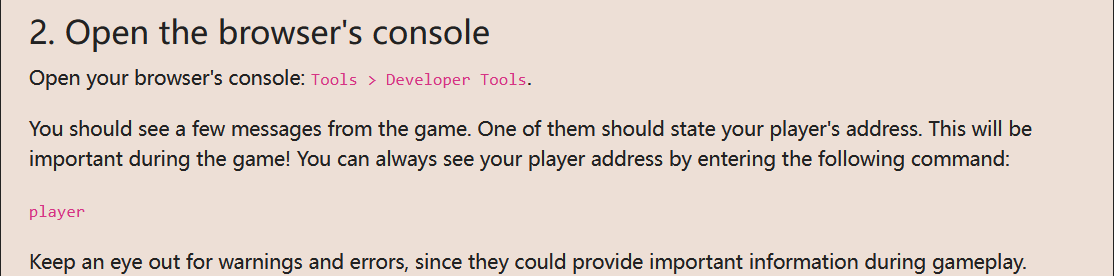
打开控制台看到的界面。

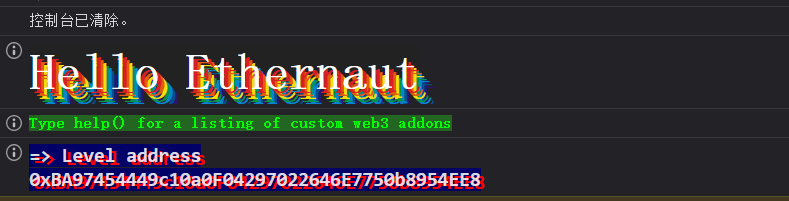
这个应该该level的token。

然后可以通过player查看自己的token。

话说这个要导入吗……emm，暂且先不导入啥的，继续往下看看吧。

使用console help()

调用help()直接查看大概的函数。

智能合约？

Solidity — Solidity 0.8.20 documentation (soliditylang.org)

http://remix.ethereum.org/#optimize=false&runs=200&evmVersion=null

火狐调用的话，好像是ethereum。

emm，先往下继续看看。

不太对，火狐应该调用的函数不变，但不知道为什么火狐无法调用。

emm，似乎因为没有测试币导致无法new instance，不是吧不是吧，真是这种神奇原因嘛？？？

真好，去水龙头那整测试币，肉眼可见电脑快窒息挂机了。

230425

"""
如果16进制是小写的形式，注意第2个参数要变成True
"""
hexstr = '2f2f3130322f2f3130382f2f39372f2f3130332f2f3132332f2f35372f2f35322f2f35322f2f3130322f2f39392f2f3130322f2f39392f2f35332f2f35302f2f39372f2f3130322f2f39372f2f3130302f2f35362f2f35362f2f34382f2f35322f2f35302f2f35352f2f35342f2f39392f2f3130312f2f34392f2f35372f2f39392f2f35312f2f35352f2f35302f2f3130302f2f35342f2f35302f2f35372f2f313235'
import base64
charstr = base64.b16decode(hexstr, True).decode()
flag_list = charstr.split('//')[1:]
# print(flag_list)
flag = ''
for i in flag_list:
    flag += chr(int(i))
    print(flag)

现代密码学及数字加密技术

现代密码学介绍
对称/非对称加密算法
消息摘要/数字签名算法

$$
signature_A \equiv H(M)^{d1} \mod n1
$$

$$
verify \equiv (signature_A)^{e1} \mod n1
$$

Eth准备？

测试币啊测试币。

Fallback

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;

contract Fallback {

  mapping(address => uint) public contributions;
  address public owner;

  constructor() {
    owner = msg.sender;
    contributions[msg.sender] = 1000 * (1 ether);
  }

  modifier onlyOwner {
        require(
            msg.sender == owner,
            "caller is not the owner"
        );
        _;
    }

  function contribute() public payable {
    require(msg.value < 0.001 ether);
    contributions[msg.sender] += msg.value;
    if(contributions[msg.sender] > contributions[owner]) {
      owner = msg.sender;
    }
  }

  function getContribution() public view returns (uint) {
    return contributions[msg.sender];
  }

  function withdraw() public onlyOwner {
    payable(owner).transfer(address(this).balance);
  }

  receive() external payable {
    require(msg.value > 0 && contributions[msg.sender] > 0);
    owner = msg.sender;
  }
}

TWO targets

you claim ownership of the contract
you reduce its balance to 0

第一个即拿到该合约的所有权，receive()函数给合约转一笔账，所有者即变成自己。

倒推以下：reveive() <- contributions() <-

窒息，烦死，被ban了好烦人。

回家用电脑整活吧嗨。

230516

用户A先选择一条椭圆曲线$E_q(a, b)$，然后选择其上的一个生成元G，假设其阶为$n$，之后再选择一个正整数$n_a$作为密钥，计算$P_a = n_a G$。

其中，$E_q(a, b)$，$q$，$G$都会被公开。

公钥为$P_a$，私钥为$n_a$。

椭圆曲线加密，加解密过程：
椭圆曲线Ep(a,b)（p为模数），基点G(x,y)，G点的阶数n，私钥k，公钥K(x,y)，随机整数r，明文为一点m(x,y)，密文为两点c1(x,y)和c2(x,y)
（其中基点G，明文m，密文c1、c2都是椭圆曲线E上的点）
选择私钥k（k<n）
得到公钥K = k*G
选择随机整数r（r<n）
加密：
c1 = m+r*K
c2 = r*G
解密：m = c1-k*c2

230525

game

各自拿硬币

++ 3
– 1
+- (-2)

亮硬币，赢面为50%。

proof：
$$
\frac{1}{4} \times 3 + \frac{1}{4} \times 1 + \frac{1}{2}\times (-2) = 0
$$
假定：

人员	正面	反面
A	$\frac{3}{8}$	$\frac{5}{8}$
B	$x$	$1-x$

预期：

情况	概率	收入
正正	$\frac{3}{8}x$	3
正反	$\frac{3}{8}(1-x)$	-2
反正	$\frac{5}{8}x$	-2
反反	$\frac{5}{8}(1-x)$	1

计算的预期为$-\frac{1}{8}$，等于说每轮都在亏损。

230531

OTP-MTP攻击

Coppersmith-Short pad攻击

230601

Rust

安装Rust

步骤忘记录了，直接查看是否运行成功。

已转移。

230605

数据处理

涉及数据脱敏，数据查找等相关代码算法。

数据生命周期

静态数据生命周期

动态数据生命周期

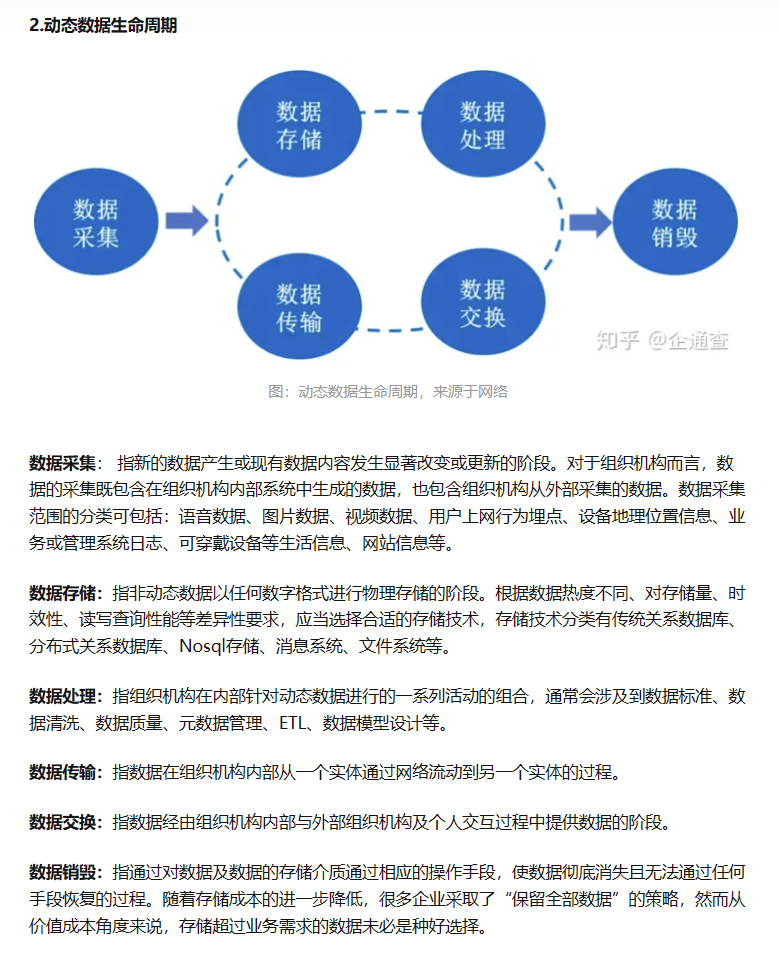
数据传输

数据传输三要素

230609

切割图片

图片分割 - 图文工具箱 - imgtool.net

montage

1	montage *.png -tile 10x10 -geometry +0+0 flag.png

10×10，表示该图片大小，理论上应该有100张图片
+0+0，表示边框为0，通常情况下使用该命令

230625

精通正则表达式

匹配：至少一位数字（0到9的任意组合）开始，接下来是字符a，接下来是字符b，最后以字符c结尾。

完整的正则表达式由两种字符构成。特殊字符称为”元字符“，其他为普通文本字符。

1
2
3

# 上面图片举例
普通字符：0 9 a b c
元字符：^ [ ] - + $

读正则表达式时遇到元字符将他解释成为其对应的普通字符，这样就能够理解记忆而不是死记硬背。

行的起始与结束

^：用于将匹配文本锚定在一行的开头
$：用与将匹配文本锚定在一行的结尾

1
2
3

^cat 匹配以c作为一行的第一个字符，紧接着一个a, 紧接着一个t的文本
cat$ 匹配以字符cat为一行结尾的文本
^$ 匹配空行，没有任何字符

字符组与排除字符组

[]：匹配方括号中的若干字符之一

gr[ae]y 匹配字符串gray 或者 grey
H[1-6] 字符组元字符'-'表示一个范围，匹配H1,H2,H3,H4,H5,H6
[0-9A-Z_!.?] 匹配一个数字，大写字母，下划线，惊叹号，点号，或者是问号
[-_.?] 匹配连字符，下划线，点号，问号

TIPS：

字符组以外的普通字符都有“接下来是”的意思，字符组的内容是在同一个位置能够匹配若干字符，它的意思是“或”。
连字符-只有在字符组内部并且没有出现在字符组的开头，它才是字符组元字符, 用来表示一个范围，否则它就只能匹配普通的连字符号。
字符. ? 在字符组外是元字符，但在字符组内他们都被当作普通字符。
[^]：匹配一个除了括号中任何未列出的字符

1 2	[^1-6] 匹配除了1到6以外的任何字符 q[^u] 匹配q后面紧接着一个除了u以为的任何一个字符

用点号匹配任意字符

.：匹配任意字符

1 2	03[-./]19[-./]76 匹配03-19-76, 03.19.76, 03/19/76 03.19.76 匹配03-19-76, 03.19.76, 03/19/76

TIPS：

在字符组中的.并不是元字符，而是普通字符点号
在字符组中的-也不是元字符，因为它在字符组的第一个位置
在字符组外的.是一个元字符，可以匹配任意字符包括普通字符点号
第一个匹配更加精确，但是更难读，也更难写。第二个匹配更容易理解，但是不够细致。使用哪一个正则表达式，取决于你对检索文本的了解，以及你需要达到的准确程度。写正则表达式时，我们需要在对欲检索文本的了解程度与检索精确性之间求得平衡。

多选结构

|：匹配分割两边的任意一个表达式
()：划定多选结构的作用范围

# 匹配grey 或者 gray
gr[ea]y
grey|gray
gr(a|e)y

# 匹配Jeffrey 或者Jeffery
Jeffrey|Jeffery 
Jeff(rey|ery)
Jeff(re|er)y

# 匹配以From,Subject或者Date开头紧跟着冒号的字符串
^(From|Subject|Date):

TIPS：

一个字符组只能匹配目标文本中的单个字符，而每个多选结构自身都可能是完整的正则表达式，都可以匹配任意长度的文本。
字符组基本可以算是一门独立的微型语言，对于元字符，它们有自己的规定。而多选结构是正则表达式语言主体的一部分。

单词分界符

\<：匹配单词的起始位置
\>：匹配单词的结束位置

1	\<cat\> 匹配单词cat

TIPS：

<和>本身并不是元字符，只有当它们与斜线结合起来的时候，整个序列才具有特殊意义，它们被称为元字符序列。
在某些语言或者工具中\b 用来表示单词分界符

可选项元素

?：表示在它之前的字符可有可无

1 2	colou?r 匹配color 或者 colour July? 匹配Jul 或者 July

量词

+ 在它之前紧邻的元素出现一次或任意多次
* 在它之前紧邻的元素出现任意多次或者不出现

1	<hr +size=[0-9]+ *> 匹配在size之前至少有一个空格，在=之后至少有一个数字，在>之前有任意多个空格

匹配优先量词 (匹配尽可能多的内容)
* + ? {min, max}
忽略优先量词 (匹配尽可能少的内容)
*? +? ?? {min, max}?
占有优先量词 (类似固化分组，一旦匹配到某些内容就固定下来不会交还)
*+ ++ ?+ {min, max}+

区间量词

{min, max} 表示在它之前的元素最少出现min次，最多出现max次

1	[a-zA-Z]{1,5} 匹配1到5个大小写字母

分组与反向引用

() 捕获分组,能够记住子表达式匹配的文本
\1 引用第一组圆括号匹配的文本
\2 引用第二组圆括号匹配的文本

1 2	\<([A-Za-z]+) +\1\> 匹配重复的单词，如 the the ([a-z])([0-9])\1\2 匹配一个字母紧接一个数字，接下来重复之前匹配的字母和匹配的数字如：a1a1

非捕获型分组 (?:)
表示只分组不捕获, 提高匹配效率并且无法引用匹配内容

(?:[a-z])

命名捕获分组 (?<Name>)
给分组命名为Area

1	(?<Area>\d\d\d)

固化分组 (?>)
固化已经捕获的内容不会再改变

1 2	i.! 可以匹配iHola! i(?>.)! 无法匹配iHola! 由于正则引擎匹配时，*已经匹配到!, 已经固化，无法再撤销重新匹配

条件判断 (?if then |else)
if 部分为特殊的条件表达式，then 和else 部分为普通的子表达式，如果if部分测试为真，则尝试then的表达式，否则尝试else部分。else 部分也可以不出现，并且省略|。
if部分因正则流派不同而不同，但大多数都容许在其中引用捕获的子表达式和环视结构。
- 使用引用作为if条件
1
2
3
( <A\s+[^>]+> \s* )? # 匹配开头的<A> tag, 如果存在的话
<IMG\s+[^>]+> # 匹配<IMG> tag
(?(1)\s*</A>) # 匹配结尾的</A>, 如果之前匹配过<A>
- 使用环视结构作为if条件
1
(?(?<=NUM:)\d+|\w+) // 它会在NUM: 之后的位置尝试匹配\d+, 但是在其他位置尝试使用\w+

转义符

在元字符前面使用反斜线称为转义符。

\. 转义点号，使它失去元字符的含义，表示一个普通的点号字符
\( 转义圆括号，使它失去分组的作用，作为普通字符的字符

1	$[a-zA-Z]+$ 匹配在一个括号内的单词如: (very)

环视结构

环视结构不占用字符，只匹配文本中的特定位置，类似与^匹配行的开头位置

(?=) 肯定顺序环视，子表达式能够匹配右侧文本则匹配位置成功
(?!) 否定顺序环视，子表达式不能匹配右侧文本则匹配位置成功
(?<=) 肯定逆序环视，子表达式能够匹配左侧文本则匹配位置成功
(?<!) 否定逆序环视，子表达式不能匹配左侧文本则匹配位置成功

s/\bJeffs\b/Jeff's/g  最简单直接的方法
s/\b(Jeff)(s)\b/$1'$2/g   过于复杂
s/\bJeff(?=s\b)/Jeff'/g  使用了顺序环视，匹配到s左边的位置
s/(?<=\bJeff)(?=s\b)/'/g 同时使了顺序环视和逆序环视，匹配到'插入的位置
s/(?=s\b)(?<=\bJeff)/'/g 与上面的正则相同，只是颠倒了两个环视结构的顺序匹配结果不受影响

TIPS：

\b 在上面的正则表达式中表示单词分界符
$1 在Perl编程语言中的正则表达式中表示反向引用第一个括号匹配的内容

其他

gr[ea]y
   解读：先找到g，接着是一个r，然后是一个a或者e，最后是一个y。
   不难看出[···]字符组元字符，代表的意思是或，更准确的说：能够匹配字符组内列出的任意
   字符，这样一来就可以把正则表达式写的更加优美简洁。但是考虑到greycolor也是匹配的，我
   们可以用上 \< 和 \> 组合元字符，来锚定单词的开始和结束。修改后的正则表达式如下：
   \<gr[ea]y\>

   字符组元字符能解决很多问题，
   1. [Ss]imon可以用来解决大小写的问题
   2. 如果我想匹配0-9中的任意一个字符我可以很快的写出:
   [0123456789] // 说好的简洁优美呢？ 
   [0-9] //优化后，怎么还不够优化？
   \d //这个整体算是一个元字符，但是它由两个字符组成，可以称为：组合元字符，等价于[0-9]

查看无线网密码

netsh wlan show profile
netsh wlan export profile folder=D:\ key=clear
netsh wlan show profile [WiFi名称] key=clear

二维码的版本问题

二维码官方叫版本为Version。
二维码一共有40个尺寸。Version 1是21 x 21的矩阵，Version 2是 25 x 25的矩阵，Version 3是29的尺寸，每增加一个version，就会增加4的尺寸，公式是：(V-1)*4 + 21（V是版本号）最高Version 40，(40-1)*4+21 = 177，所以最高是177 x 177 的正方形。

version2 二维码的标准大小应该是25x25。想到零宽字节隐写。

rar

rar5.0加密

上面说的两种工具没办法破解rar5.0的加密，不过可以用破解版的Accent RAR Password Recovery进行爆破，这个工具也支持暴力破解、掩码爆破、字典爆破。

或者先用john获取rar文件的hash值，再用hashcat爆破

rar文件格式

RAR 5.0 archive format (rarlab.com)

下面的文件格式分析是基于RAR4.x，并不是RAR5.0
RAR 5.0签名和RAR4.x的签名不一样
RAR 5.0签名由8个字节组成:
0x52 0x61 0x72 0x21 0x1A 0x07 0x01 0x00
比较一下
RAR 4.x 签名由7字节组成:
0x52 0x61 0x72 0x21 0x1A 0x07 0x00

常见的块

标记块：HEAD_TYPE=0x72
压缩文件头：HEAD_TYPE=0x73
文件头：HEAD_TYPE=0x74
旧风格的注释头：HEAD_TYPE=0x75
旧风格的用户身份信息：HEAD_TYPE=0x76
旧风格的子块：HEAD_TYPE=0x77
旧风格的恢复记录：HEAD_TYPE=0X78
旧风格的用户身份信息：HEAD_TYPE=0X79
子块：HEAD_TYPE=0x7A
最后的结束块：HEAD_TYPE=0x7B

Kali自带密码字典rockyou.txt解压

找位置

1	/usr/share/wordlists

wordlists中解压

1	sudo gzip -d /usr/share/wordlists/rockyou.txt.gz

john

密码破解-john的使用 - Junglezt - 博客园 (cnblogs.com)

hashcat

密码破解-hashcat的简单使用 - Junglezt - 博客园 (cnblogs.com)

[example_hashes hashcat wiki]

hashcat - advanced password recovery

修改内核。

230803

coppersmith下限

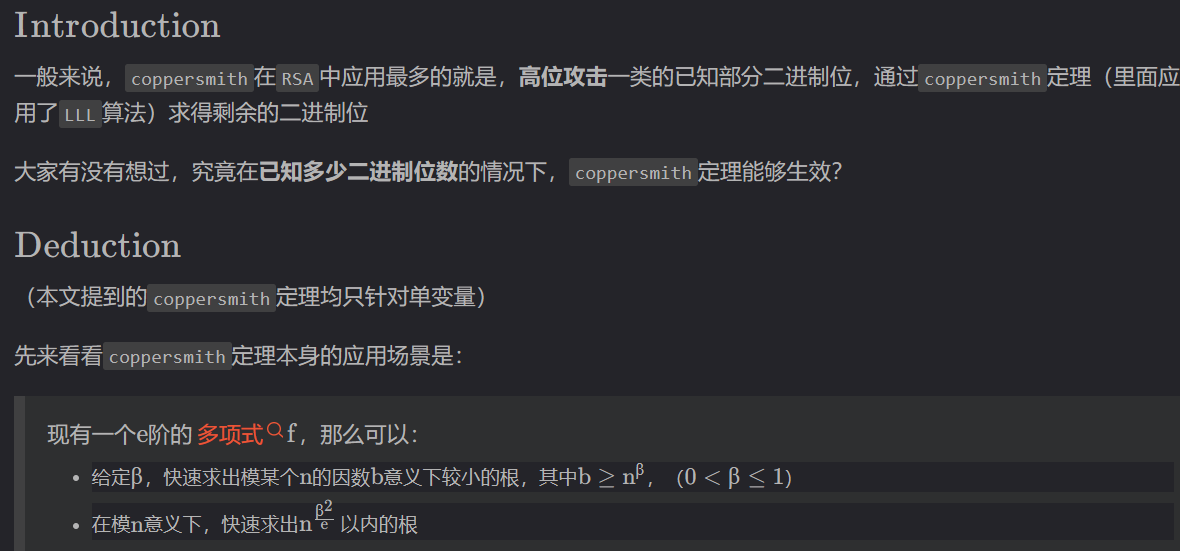
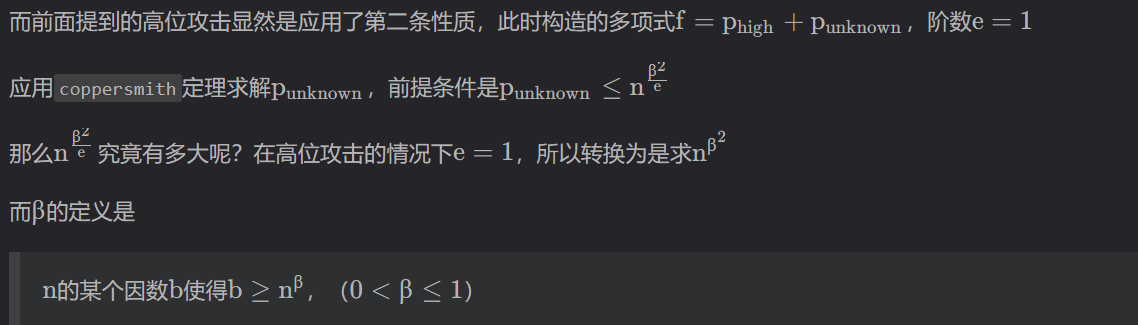
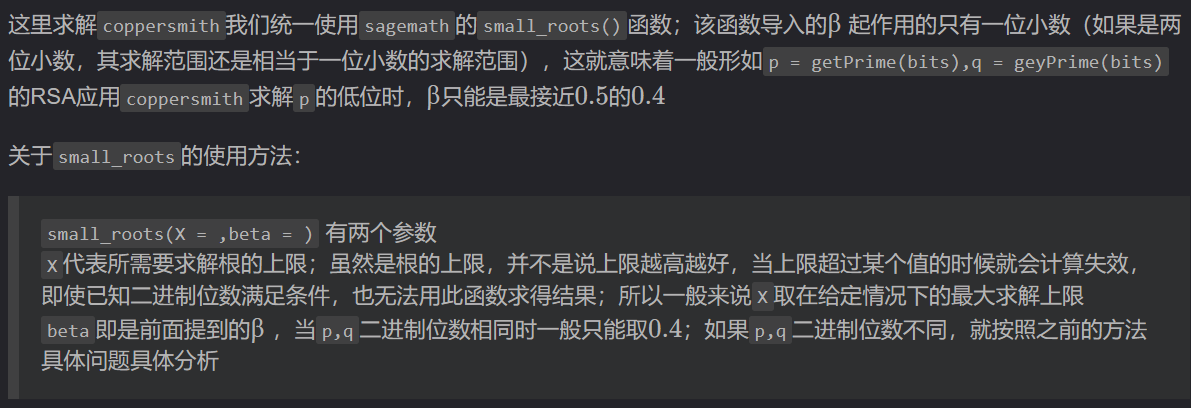
在sagemath中应用coppersmith定理的函数有两个：small_roots， coppersmith_howgrave_univariate。
这里求解coppersmith我们统一使用sagemath的small_roots()函数；该函数导入的 $\beta$起作用的只有一位小数（如果是两位小数，其求解范围还是相当于一位小数的求解范围），这就意味着一般形如p = getPrime(bits),q = geyPrime(bits)的RSA应用coppersmith求解$p$的低位时，$\beta$只能是最接近$0.5$ 的$0.4$。

关于small_roots()的使用方法：

1	small_roots(X = ,beta = ) 有两个参数

$X$代表所需要求解根的上限；虽然是根的上限，并不是说上限越高越好，当上限超过某个值的时候就会计算失效，即使已知二进制位数满足条件，也无法用此函数求得结果；所以一般来说$X$取在给定情况下的最大求解上限。

$beta$即是前面提到的$\beta$ ，当$p$,$q$二进制位数相同时一般只能取$0.4$；如果$p$,$q$二进制位数不同，就按照之前的方法具体问题具体分析。

经过测试得到，当未知量小于等于$454bits$时（$p$,$q$为$1024bits$），coppersmith定理可以求解

之后改变了$p$,$q$的大小，经过测试发现，当$p$,$q$同二进制位数时，要使用small_roots()应用coppersmith定理求解$n$的某个因数的低位，需要满足未知的二进制位数与因数之间的二进制位数的关系是：
$$
bits_{unknown} \div bits_{p} < = 0.44
$$

230807

230808

mysql赋权操作

1	GRANT ALL PRIVILEGES ON . TO 'root'@'%' IDENTIFIED BY '123456' WITH GRANT OPTION;

GRANT：赋权命令
ALL PRIVILEGES：当前用户的所有权限
ON：介词
*.*：当前用户对所有数据库和表的相应操作权限
TO：介词
'root'@'%'：权限赋给root用户，所有ip都能连接
IDENTIFIED BY ‘123456’：连接时输入密码，密码为123456
WITH GRANT OPTION：允许级联赋权

正则表达式

练习网站：

Regex Golf (alf.nu)

RegexOne - Learn Regular Expressions - Lesson 1: An Introduction, and the ABCs

参考答案：

Regex Golf 正则表达式练习（持续更新）_regex golf的it never ends_NJYR21的博客-CSDN博客

正则表达式练习(Regex Golf)_regex golf答案_强强学习的博客-CSDN博客

git练习

Learn Git Branching

教程

translations/README-cn.md · master · mirrors / ziishaned / learn-regex · GitCode

230809-230810

正则匹配练习-RegexOne

RegexOne - Learn Regular Expressions - Problem X: Infinity and beyond!

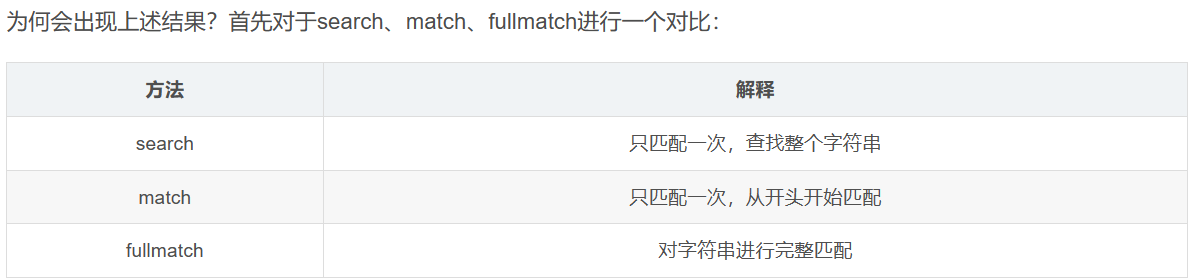
简写	描述
.	除换行符外的所有字符
\w	匹配所有字母数字，等价于[a-zA-Z0-9_]
\W	匹配所有非字母数字，即符号，等价于`[^\w]`
\d	匹配数字[0-9]
\D	匹配所有非数字，等价于`[^\D]`
\s	匹配所有空格字符，等价于`[\t\n\f\r\p{Z}]`
\S	匹配所有非空格字符，等价于`[^\s]`
\f	匹配一个换页符
\n	匹配一个换行符
\r	匹配一个回车符
\t	匹配一个制表符
\v	匹配一个垂直制表符
\p	匹配 CR/LF（等同于 \r\n ），用来匹配 DOS 行终止符

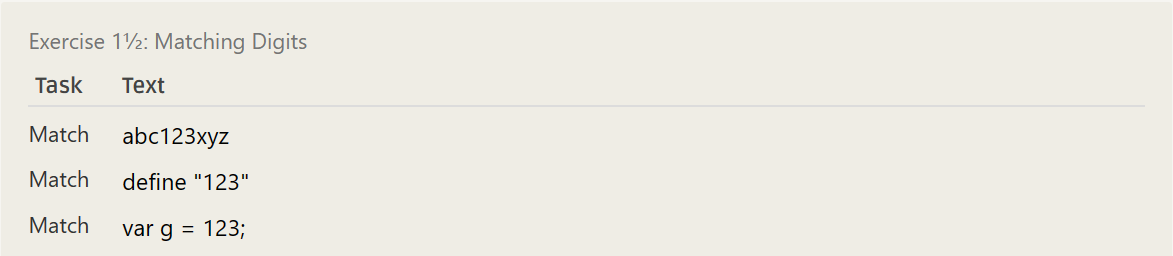
123
……

\.
...\.
……

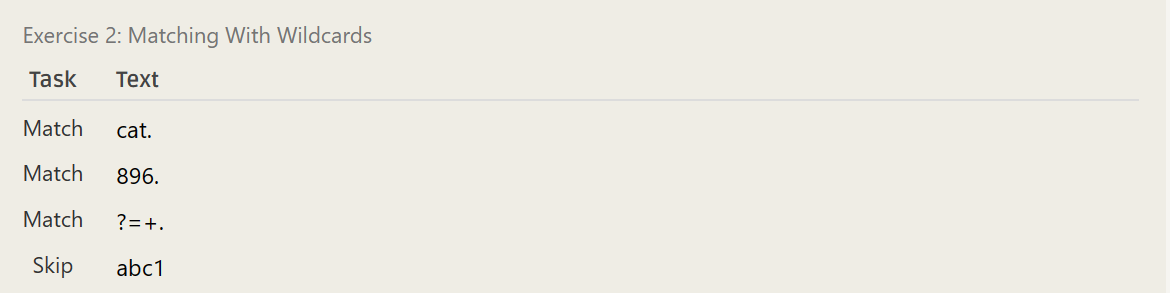
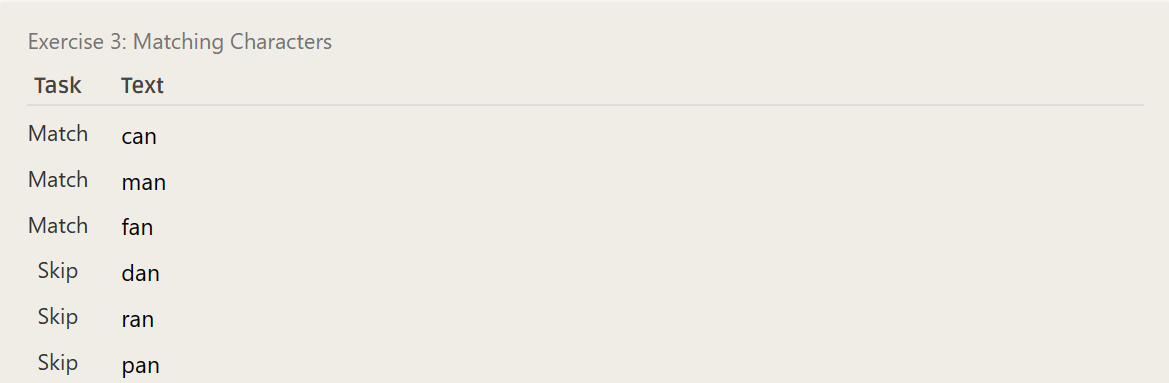
[cmf]an
[^drp]an
……

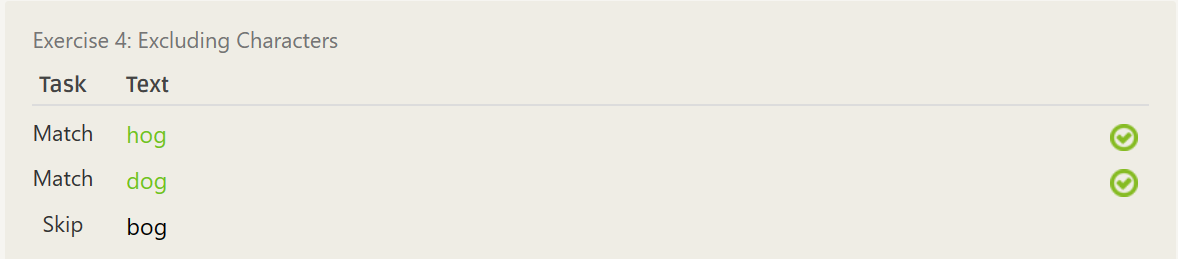
[^b]og
[hd]og
……

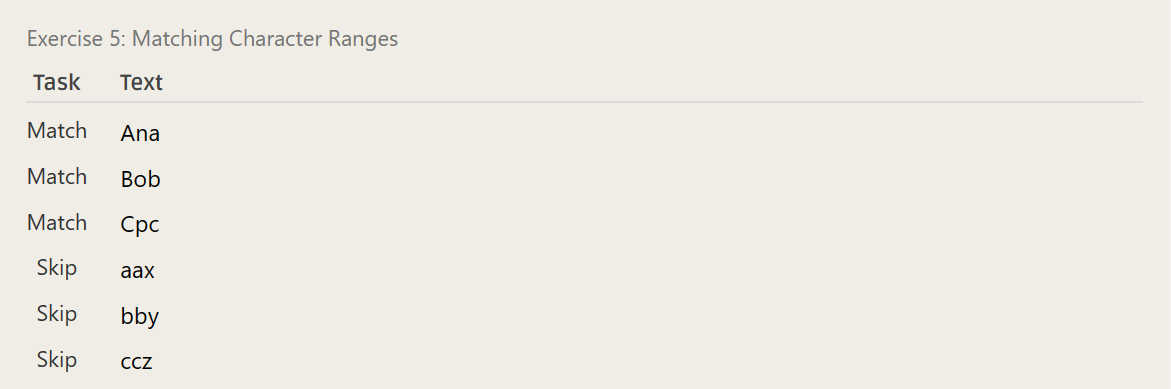
[A-Z][nop][a-c]
[A-Z]
……

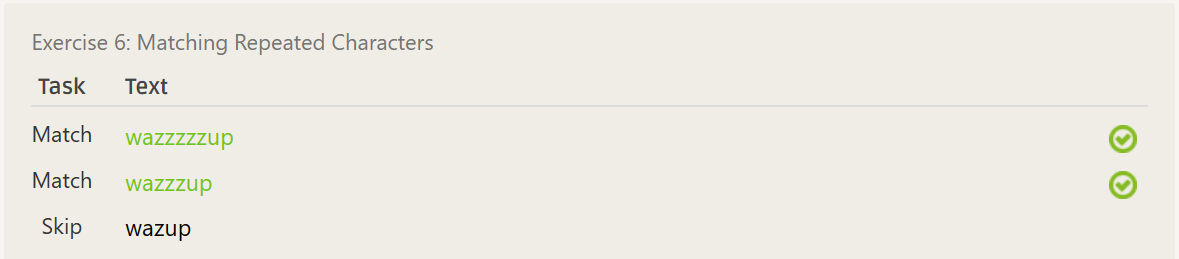
waz{3,5}up
……

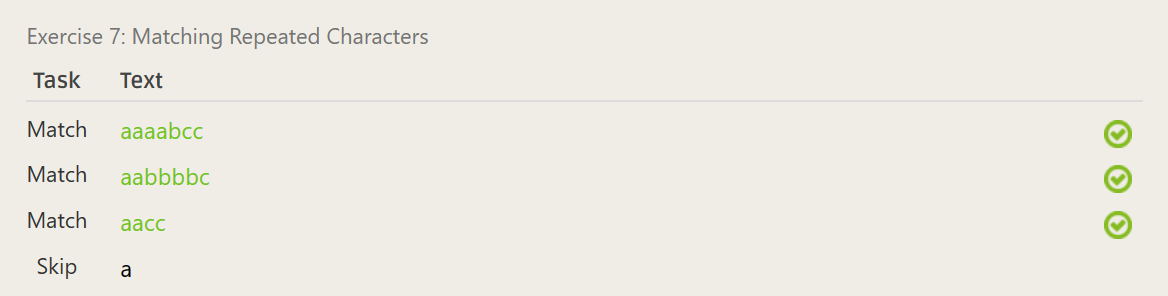
a+b*c+
aa
a{2,4}b{0,4}c{1,2}
……

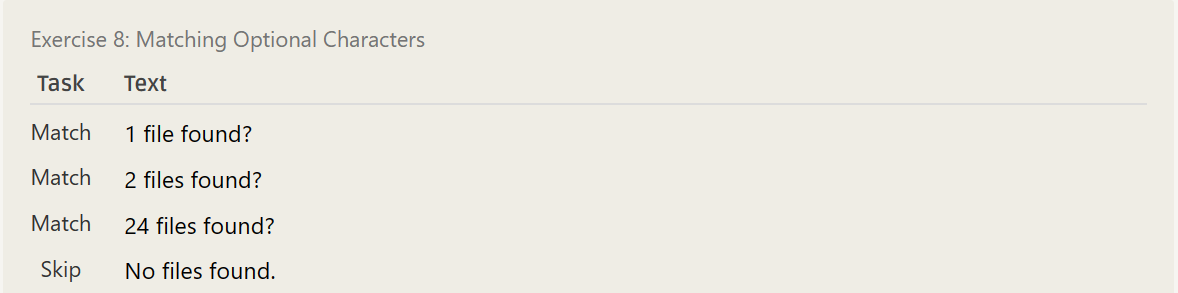
[0-9]\sfile(s|\s)
\d+ files? found\?
……

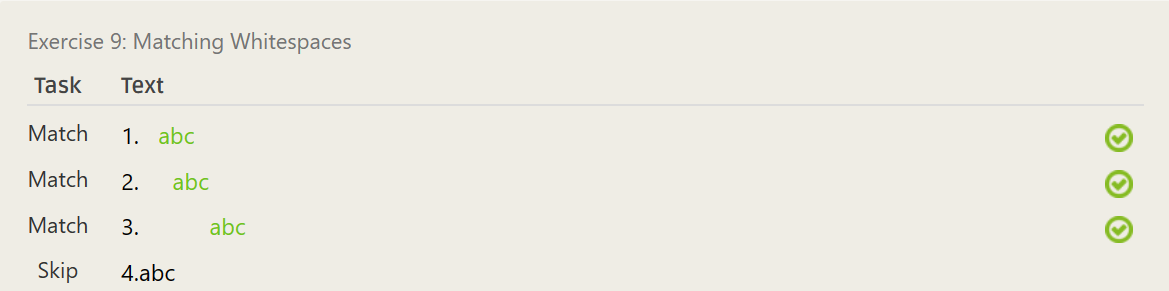
\d\.\s+abc
[\s]
[^\S]
[0-9]\.\s+[a-c]+
……

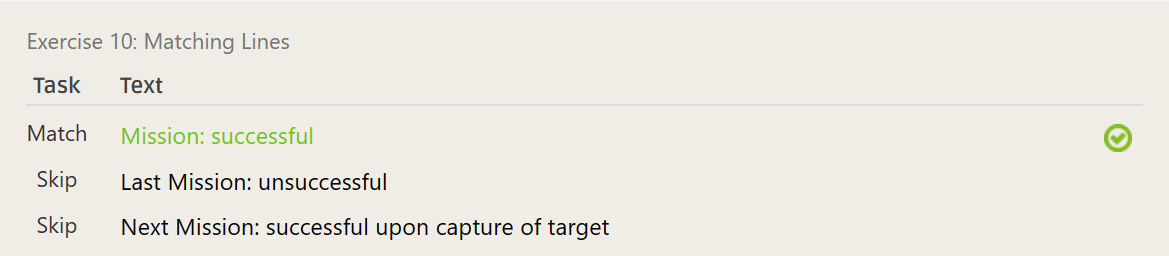
(^M)[a-z]+: \w+
(^M)\w+: \w+
^Mission: successful$
(^Mission): [a-z]+
……

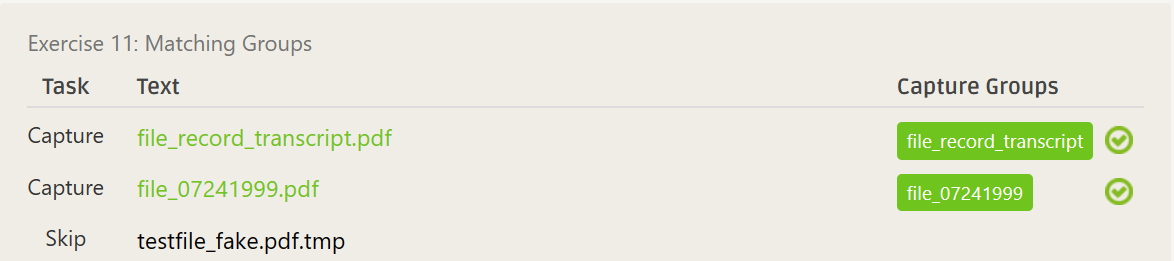
^(file.+)\.pdf
^(file.*)\.pdf
……

(\w+\s(\d+))
(\w+ (\d+))
……

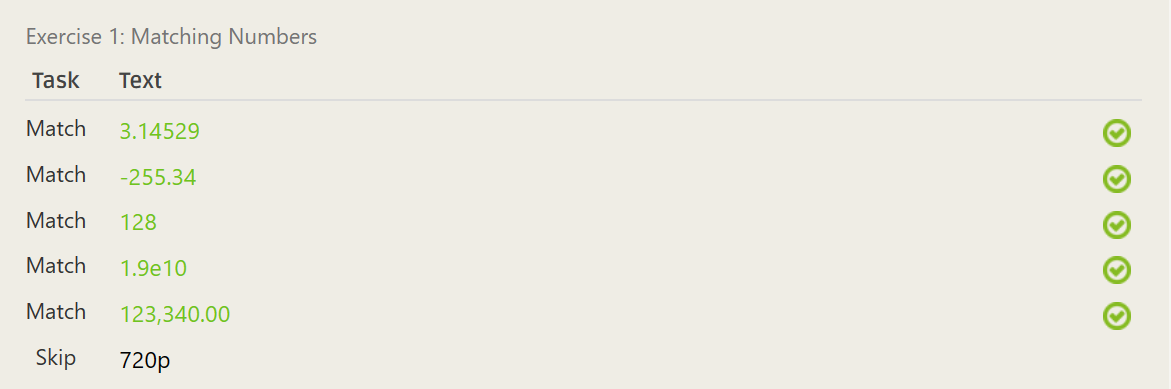
[^p]$
^-?\d+(,\d+)*(\.\d+(e\d+)?)?$
……

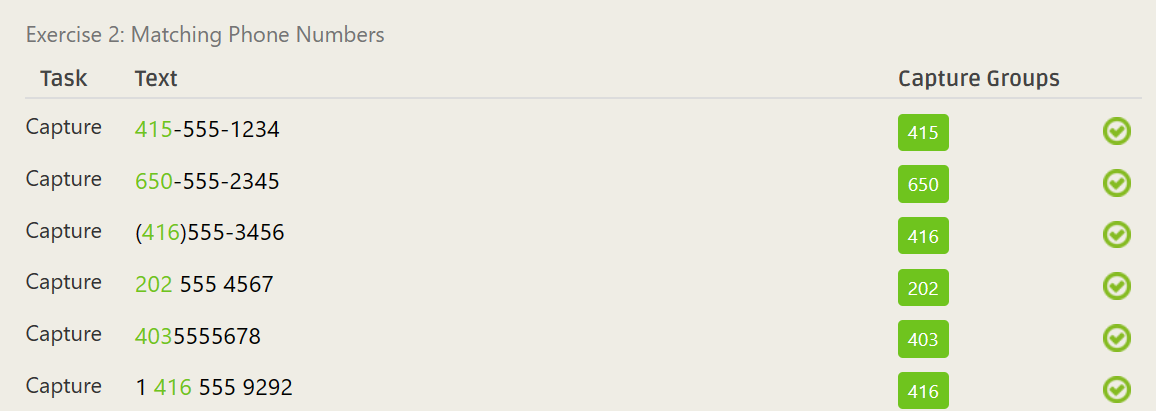
(\d{3})
1?[\s-]?$?(\d{3})$?[\s-]?\d{3}[\s-]?\d{4}
……

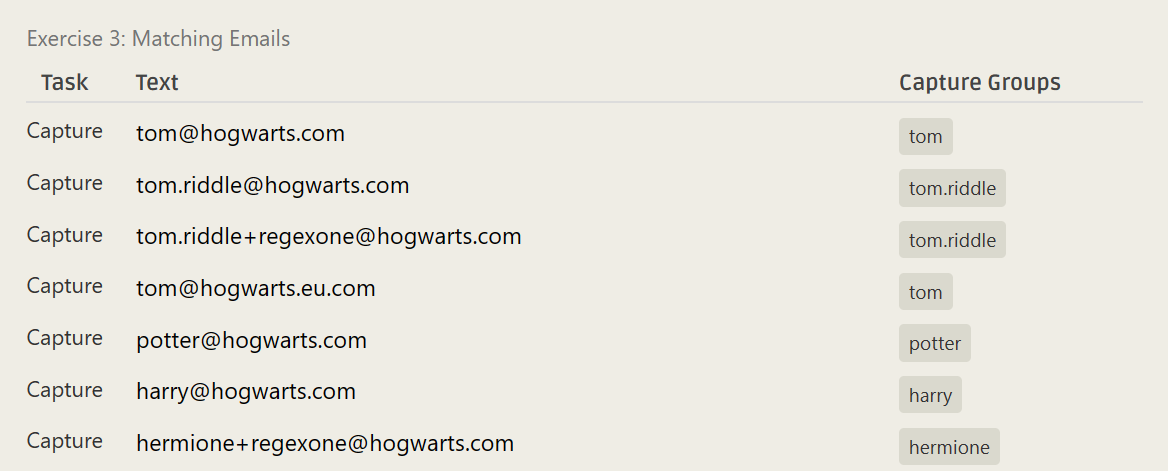
^([\.\w]*)
^([\.\w]*)[\W\w]+$
……

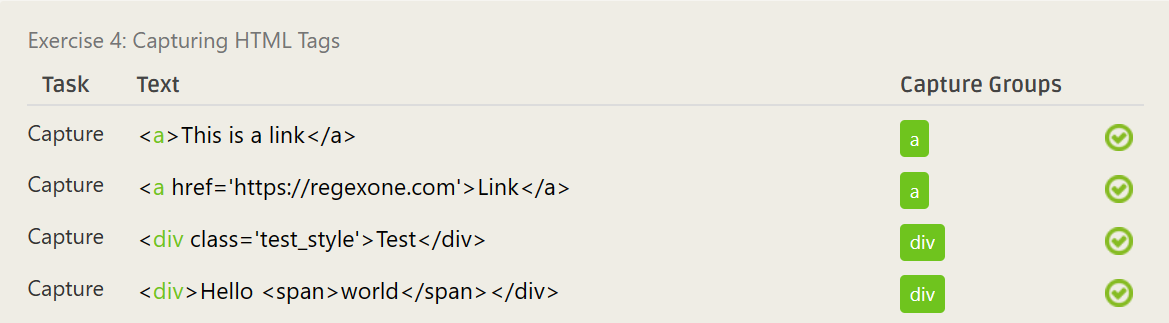
(\w{1,3})
\<([\w]{1,3})[\>\s]?[\w]+\=?[\W\w]+
……

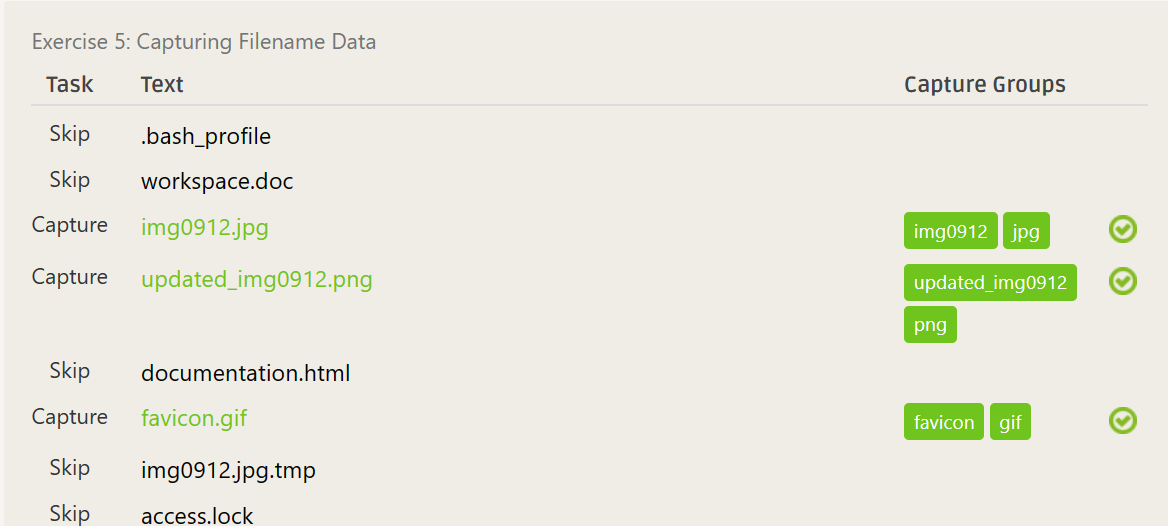
^(\w+)\.?(png|jpg|gif)$
……

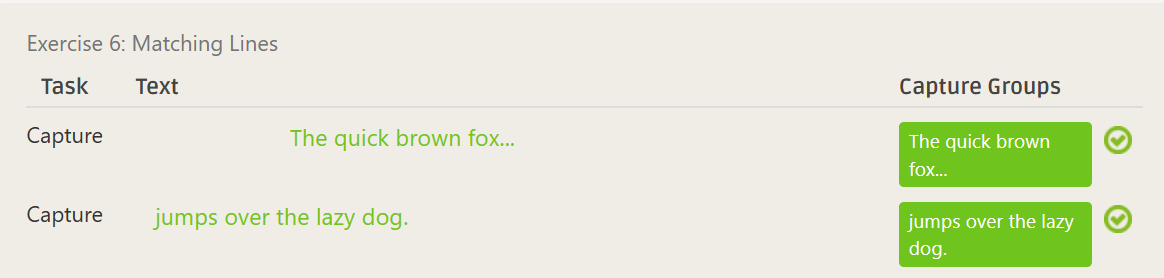
[\s]+(.*)
^\s*(.*)\s*$
……

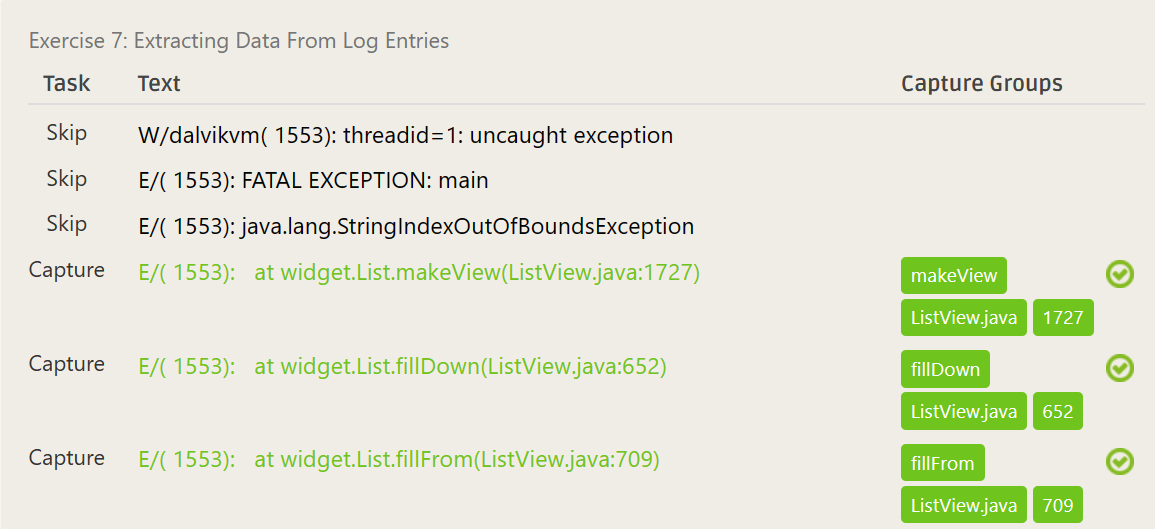
.*\.(\w+)$([\w\.]+):(\d+)$
(\w+)$([\w\.]+):(\d+)$
……

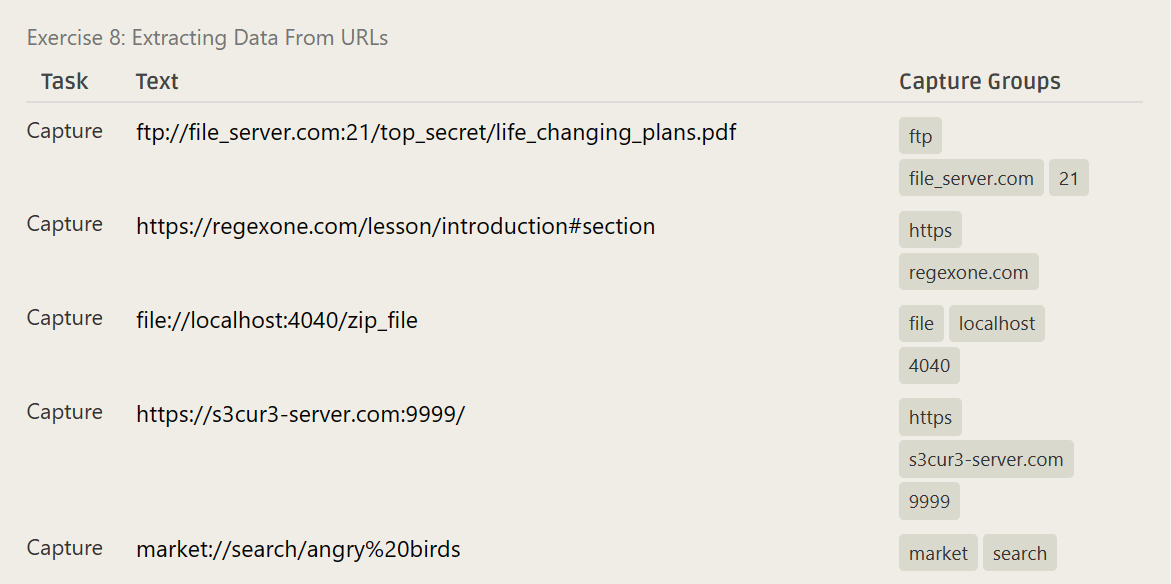
(\w+)://([\w\.-]+)[:]?(\d+)?
(\w+)://([\w\-\.]+)(:(\d+))?
^(\w+)://([\w\.-]+)[:]?(\d+)?.*$
……

230818

正则匹配进阶

锚点

^用来检查匹配的字符串是否在所匹配字符串的开头。
同理于 ^号， $号用来匹配字符是否是最后一个。例如，(at\.)$ 匹配以at.结尾的字符串。

零宽度断言

先行断言和后发断言（合称 lookaround）都属于非捕获组（用于匹配模式，但不包括在匹配列表中）。当我们需要一个模式的前面或后面有另一个特定的模式时，就可以使用它们。

例如，我们希望从下面的输入字符串 $4.44 和 $10.88 中获得所有以 $ 字符开头的数字，我们将使用以下的正则表达式 (?<=\$)[0-9\.]* 。意思是：获取所有包含 . 并且前面是 $ 的数字。

零宽度断言

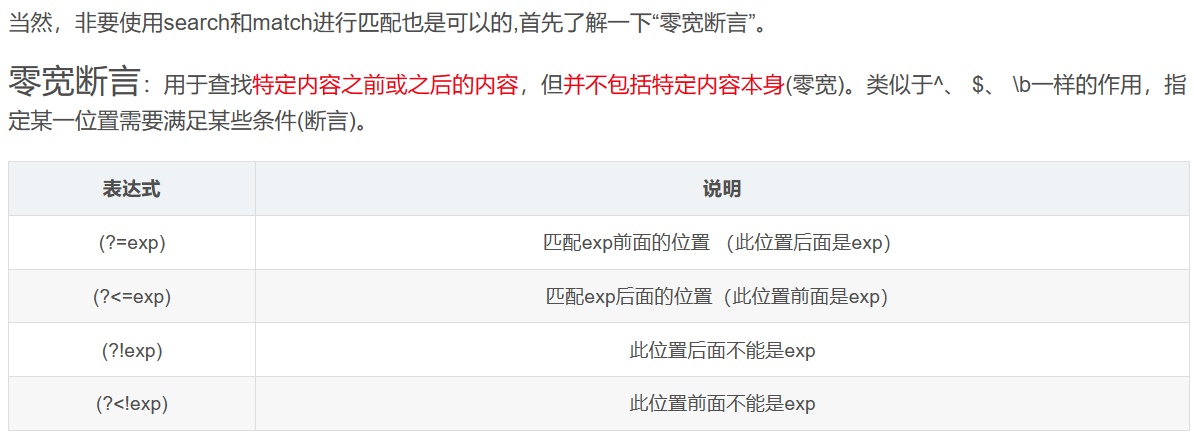
符号	描述
?=	正先行断言-存在
?!	负先行断言-排除
?<=	正后发断言-存在
?<!	负后发断言-排除

`?=`正先行断言-存在

?= 正先行断言，表示第一部分表达式之后必须跟着 ?= 定义的表达式。

返回结果只包含满足匹配条件的第一部分表达式。

定义一个正先行断言要使用 () 。在括号内部使用一个问号和等号： (?=...) 。

正先行断言的内容写在括号中的等号后面。

`?!`负先行断言-排除

负先行断言?!用于筛选所有匹配结果，筛选条件为其后不跟随着断言中定义的格式。

正先行断言定义和负先行断言一样，区别就是=替换成!也就是 (?!...) 。

`?<=`正后发断言-存在

正后发断言记作(?<=...)用于筛选所有匹配结果，筛选条件为其前跟随着断言中定义的格式。

`?<!`负后发断言-排除

负后发断言记作(?<!...)用于筛选所有匹配结果，筛选条件为其前不跟随着断言中定义的格式。

标志

标志也叫模式修正符，因为它可以用来修改表达式的搜索结果。

这些标志可以任意的组合使用，它也是整个正则表达式的一部分。

标志	描述
i	忽略大小写
g	全局搜索
m	多行修饰符：锚点元字符`^`，`$`工作范围在每行起始

忽略大小写

修饰语i用于忽略大小写。

全局搜索

修饰符 g 常用于执行一个全局搜索匹配，即（不仅仅返回第一个匹配的，而是返回全部）。

多行修饰符

多行修饰符 m 常用于执行一个多行匹配。

贪婪匹配与惰性匹配

正则表达式默认采用贪婪匹配模式，在该模式下意味着会匹配尽可能长的子串。我们可以使用 ? 将贪婪匹配模式转化为惰性匹配模式。

?对其进行截断。从而减少匹配的长子串。

$$
正确率 = (\frac{提交正确条数}{提交全部条数}) \times 100
$$

$$
召回率 = (\frac{提交正确条数}{正确样本条数}) \times 100
$$

$$
单类型分数 = \frac{2 \times 正确率 \times 召回率}{正确率 + 召回率}
$$

$$
总分数 = \frac{1}{n}\sum_{i=1}^{n} 单类型分数_i
$$

230905

kali实现mysql运行

直接运行mysql -u root，会出现报错ERROR 2002 (HY000): Can‘t connect to local MySQL server through socket ‘/tmp/mysql.sock‘ (2)。

目前解决方法

WSL下Kali 2021 启用mysql服务并通过主机连接_kali mysql 连接另外主机_zhy_27的博客-CSDN博客

打开mysql环境sudo service mysql start
直接运行mysql
创建新的数据库：create database test;
转换到新创建的数据库：use test;
导入sql文件：source xx.sql;
查看当前数据库下的表名：show tables;
查看对应列下的数据：select xx from [tables];
关闭数据库服务：service mysql stop

spacy

每个元组由三个值构成：匹配到的ID，匹配到的跨度的起始和终止索引。

230906

特征工程以及训练模型

词向量是将字、词语转换成向量矩阵的计算模型。

目前为止最常用的词表示方法是 One-hot，这种方法把每个词表示为一个很长的向量。这个向量的维度是词表大小，其中绝大多数元素为 0，只有一个维度的值为 1，这个维度就代表了当前的词。

还有 Google 团队的 Word2Vec，其主要包含两个模型：跳字模型（Skip-Gram）和连续词袋模型（Continuous Bag of Words，简称 CBOW），以及两种高效训练的方法：负采样（Negative Sampling）和层序 Softmax（Hierarchical Softmax）。

值得一提的是，Word2Vec 词向量可以较好地表达不同词之间的相似和类比关系。除此之外，还有一些词向量的表示方式，如 Doc2Vec、WordRank 和 FastText 等。

特征选择

在一个实际问题中，构造好的特征向量，是要选择合适的、表达能力强的特征。文本特征一般都是词语，具有语义信息，使用特征选择能够找出一个特征子集，其仍然可以保留语义信息；但通过特征提取找到的特征子空间，将会丢失部分语义信息。

目前，常见的特征选择方法主要有 DF、 MI、 IG、 CHI、WLLR、WFO 六种。

230911

时间处理

函数	描述
time()	获取当前时间戳 \textcolor{red}{时间戳}时间戳
gmtime()	获取当前时间戳对应的 s t r u c t _ t i m e \textcolor{red}{struct_time}struct_tme 对象
localtime()	获取当前时间戳对应的本地时间 \textcolor{red}{本地时间}本地时间的 struct_time 对象
ctime()	获取当前时间戳对应的易读字符串 \textcolor{red}{易读字符串}易读字符串表示，内部会调用 time.localtime()

struct_time

下标	属性	值
0	tm_year	年份，整数
1	tm_mon	月份[1, 12]
2	tm_mday	日期[1, 31]
3	tm_hour	小时[0, 23]
4	tm_min	分钟[0, 59]
5	tm_sec	秒[0, 61]
6	tm_wday	星期[0, 6]（0表示星期一）
7	tm_yday	该年第几天[1, 366]
8	tm_isdst	是否夏时令，0否, 1是, -1未知

时间格式化

函数	描述
mktime()	将 struct_time 对象 t 转换为时间戳 \textcolor{red}{转换为时间戳}转换为时间戳
strftime()	时间格式化 \textcolor{red}{格式化}格式化
strptime()	提取字符串中的时间来生成struct_ time\textcolor{red}{struct_time}struct_time 对象

strftime()

格式化字符串	日期/时间	值范围和实例
%Y	年份	0001~9999，例如：1900
%m	月份	01~12，例如：10
%B	月名	January~December，例如：April
%b	月名缩写	Jan~Dec，例如：Apr
%d	日期	01 ~ 31，例如：25
%A	星期	Monday~Sunday，例如：Wednesday
%a	星期缩写	Mon~Sun，例如：Wed
%H	小时（24h制）	00 ~ 23，例如：12
%I	小时（12h制）	01 ~ 12，例如：7
%p	上/下午	AM, PM，例如：PM
%M	分钟	00 ~ 59，例如：26
%S	秒	00 ~ 59，例如：26

计时

函数	描述
sleep(secs)	暂停执行调用线程达到给定的秒数。参数可以是浮点数，以指示更精确的睡眠时间。实际的暂停时间可能小于请求的时间，因为任何捕获的信号将在执行该信号的捕获例程后终止 sleep() 。此外，由于系统中其他活动的安排，暂停时间可能比请求的时间长任意量。
monotonic()	返回单调时钟的值（以小数秒为单位），即不能倒退的时钟。时钟不受系统时钟更新的影响。返回值的参考点未定义，因此只有连续调用结果之间的差异才有效。
perf_counter()	返回性能计数器的值（以小数秒为单位），即具有最高可用分辨率的时钟，以测量短持续时间。它确实包括睡眠期间经过的时间，并且是系统范围的。返回值的参考点未定义，因此只有连续调用结果之间的差异才有效。

Pell方程与RSA

pell方程与群的笔记 | 独奏の小屋 (hasegawaazusa.github.io)

同构映射的性质 - 知乎 (zhihu.com)

定义1 设 $V$ 与 $V’$ 都是域 $F$ 上的线性空间，如果存在 $V$ 到 $V’$ 的一个双射 $\sigma$ ，并且 $\sigma$ 保持加法与纯量乘法两种运算，即使对于任意 $\alpha, \beta\in V$, $k \in F$，有：
$$
\sigma (\alpha + \beta) = \sigma(\alpha) + \sigma(\beta),\
\sigma (k\alpha) = k\sigma (\alpha)
$$
那么称 $\sigma$ 是 $V$ 到 $V’$ 的一个同构映射（简称为同构）；此时称 $V$ 与 $V’$ 是同构的，记作 $V \cong V’$。

从定义可以看出，如果域 $F$ 上的两个线性空间 $V$ 与 $V’$ 是同构的，那么 $V$ 与 $V’$ 的元素之间存在一一对应：$\alpha \longmapsto \sigma(\alpha)$；并且这个映射 $\sigma$ 保持加法与纯量乘法两种运算，由此可以推导出 $\sigma$ 具有下列性质：

性质1 $\sigma(0)$ 是 $V’$ 的零元。
性质2 $V$ 中的向量组 $\alpha_1, \alpha_2, \alpha_3, \cdots, \alpha_s$ 线性相关（无关），当且仅当 $\sigma(\alpha_1), \sigma(\alpha_2), \cdots, \sigma(\alpha_s)$ 是 $V’$ 中的线性相关（无关）组。
性质3 如果 $\alpha_1, \alpha_2, \alpha_3, \cdots, \alpha_n$ 是 $V$ 的一个基，那么 $\sigma(\alpha_1), \sigma(\alpha_2), \cdots, \sigma(\alpha_n)$ 是 $V’$ 的一个基。
性质4 如果 $U$ 是 $V$ 的一个子空间，那么 $\sigma(U)$ 也是 $V’$ 的一个子空间，如果 $U$ 是有限维的，那么 $\sigma(U)$ 也是有限维的，并且$dim_{\sigma_{(U)}} = dim_{U}$

判定：

定理1 域$F$上两个有限维的线性空间同构的充分必要条件是它们的维数相同。

Pell方程

定义形如 $x^{2} - Dy^{2} = 1$ 的二元二次方程，其中D为正整数。

对模 $n$ 的Pell方程，我们有：
$$
x^{2} - Dy^{2} \equiv 1 \mod n
$$
构成该方程的元素，称为群。

根据Pell方程的性质，有元素加法：
$$
(x_3, y_3) = (x_1, y_1) \oplus (x_2, y_2) = (x_1x_2 + Dy_1y_2, x_1y_2 + x_2y_1)
$$
存在数乘：

$e \otimes (x, y) = (x, y) \oplus (x, y) \oplus \cdots \oplus(x, y)$

230914

encoded

Salted__了解一下，这个是通过openssl加密如果不带base64就会出现Salted字段打头。再看base64的前几个字段U2Fsd确定是AES加密无误

AreYouOK_Pro

修改文件后缀名，修改为.pcap
协议查看，存在RFCOMM，wireshark筛选为btrfcomm
968之后的数据包存在文件传输，利用btrfcomm && data && frame.number >= 968进行筛选
将这些数据包导出为json，提取其中data段信息并扔掉报文头后，发现内容为一张图片，保存出来

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import json

packets = json.loads(open("1.json", "r").read())
data = ""
for packet in packets:
    data += packet["_source"]["layers"]["data"]["data.data"].replace(":", "")
data = data.split("a5a50100")
newdata = ""
for x in data:
    newdata += x[8:]
open("111.png", "wb").write(newdata[24:].decode('hex'))

保存后打不开，可能存在冗余信息，直接通过foremost把里面的图片提取出来，得到：

Beyond

标明ICMP存活。

数据包表示向目标主机发送了一个ICMP Echo Request消息，查看相应数据包的信息来判断主机是否存活。如果有相应的ICMP Echo Reply数据包作为响应，则表明目标主机是存活的。

使用http && http.response.code == 200进行筛选，再对其进行排序，查看相对特殊的长度，比如最长长度，追踪http流。

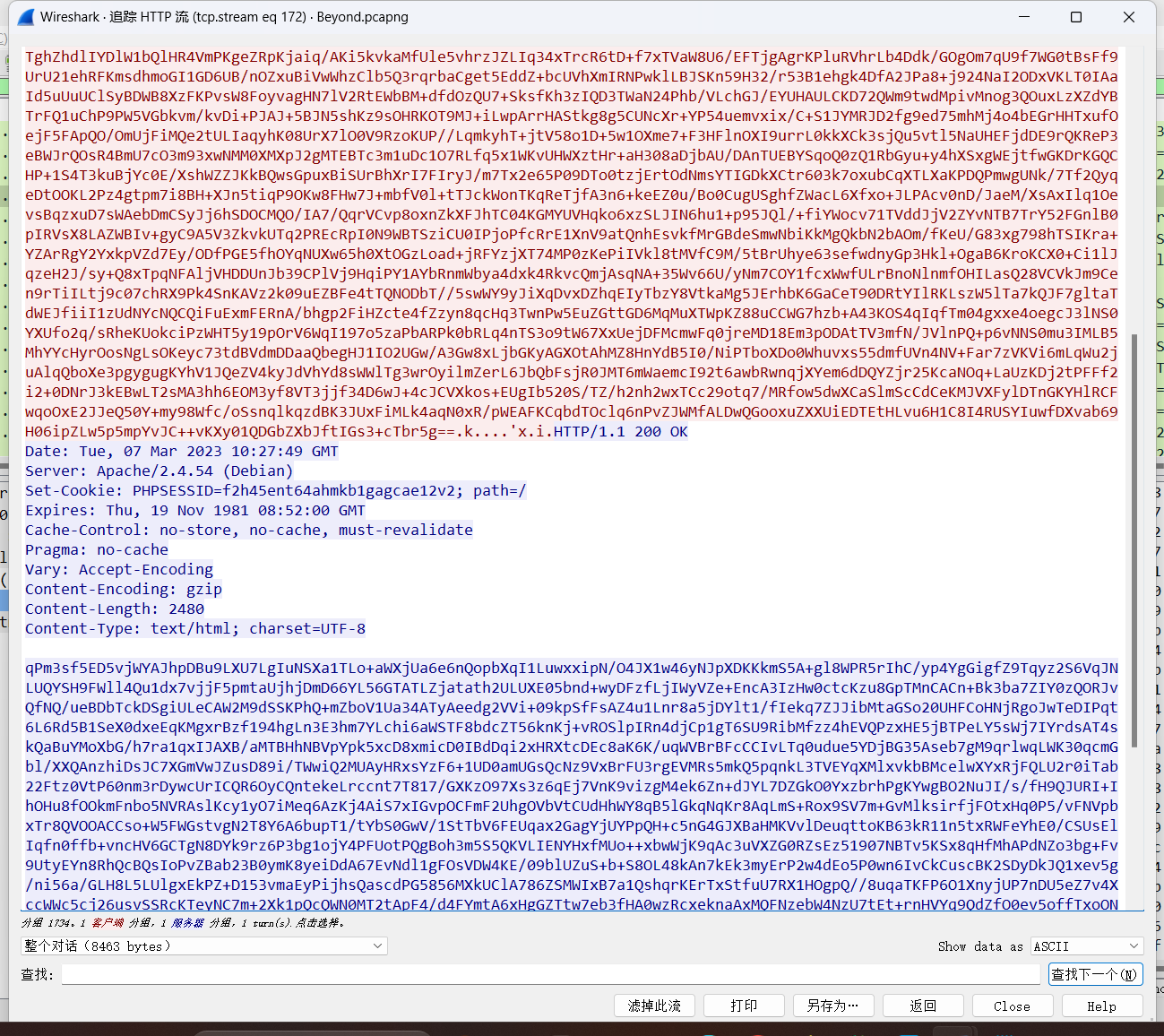
分析（官方wp），为冰蝎V4.0流量，服务端为PHP，使用默认的AES算法。

进行解密。

import re
import base64
import hashlib
from Crypto.Cipher import AES
def Decrypt(key, data):
    c = AES.new(key, AES.MODE_ECB)
    decodebs = base64.b64decode(data)
    return c.decrypt(decodebs)
# def Key_Brute(data):
# with open('top500.txt', 'rb') as f:
# plain = [i.strip() for i in f.readlines()]
# for i in plain:
# md5_enc = hashlib.md5(i).hexdigest()
# try:
# key = md5_enc[:16].encode()
# AES_dec = Decrypt(key, data).decode('utf-8')
# cmd = re.findall(r'[sS]$cmd="(.*?)"', AES_dec)
# if cmd:
# print('[*] Crack Success!!!' + 'n' + '[*] Key: ' + i.decode('utf-8') + 'n[*] Webshell Key: ' + md5_enc[:16])
# payload = base64.b64decode(cmd[0]).decode('utf-8')
# print('[*] Payload: ' + payload)
# break
# except Exception as e:
# print('[-] Crack Failed')
if __name__ == '__main__':
    data = b'xxx'
    md5_enc = hashlib.md5(b'hunting').hexdigest()
    key = md5_enc[:16].encode()
    AES_dec = Decrypt(key, data).decode('utf-8')
    print(AES_dec)

230流解密后，存在cmd等信息

231019

CryptoCTF2023

reference:

2023 CCTF — writeup-CSDN博客

2023 CryptoCTF wp by lingfeng (easy分类)-CSDN博客

一点新东西进行概括。

调用`factordb.com`的api接口，进行爆破。

from Crypto.Util.number import *
import gmpy2
import requests
from tqdm import *
PKEY = 55208723145458976481271800608918815438075571763947979755496510859604544396672
ENC = 127194641882350916936065994389482700479720132804140137082316257506737630761
c_high = ENC<<8
n_high = (PKEY>>8)<<8
e_high = (PKEY & (2**8-1))<<8
def factor_n(n):
    url = "http://factordb.com/api?query={}".format(str(n))
    try:
        response = requests.get(url)
        fac = response.json()['factors']
        fac_data = [int(i[0]) for i in fac]
        return fac_data
    except:
        pass

p_q = []
for i in trange(2**8):
    n = n_high+i
    fac_data = factor_n(n)
    if len(fac_data)==2:
        if fac_data[0].bit_length()==128 and fac_data[1].bit_length()==128 and isPrime(fac_data[0]) and isPrime(fac_data[1]):
            p_q = fac_data
            break
p,q = int(fac_data[0]),int(fac_data[1])
n = p*q
phi = (p-1)*(q-1)
for i in range(2**8):
    for j in range(2**8):
        c = c_high + i
        e = e_high + j
        if isPrime(e):
            try:
                d = gmpy2.invert(e, phi)
                m = pow(c,d,n)
                flag = long_to_bytes(m)
                if all(k<=127 and k >=33 for k in flag):
                    print(b"CCTF{"+flag+b"}")
                    break
            except:
                pass

Risk

构造方程，以及进行约束求解$a, b$从而计算出$p, q$。

231020

SCYD数据安全

Baby_TCP

GitHub - lclevy/firepwd: firepwd.py, an open source tool

231121

卷积概念

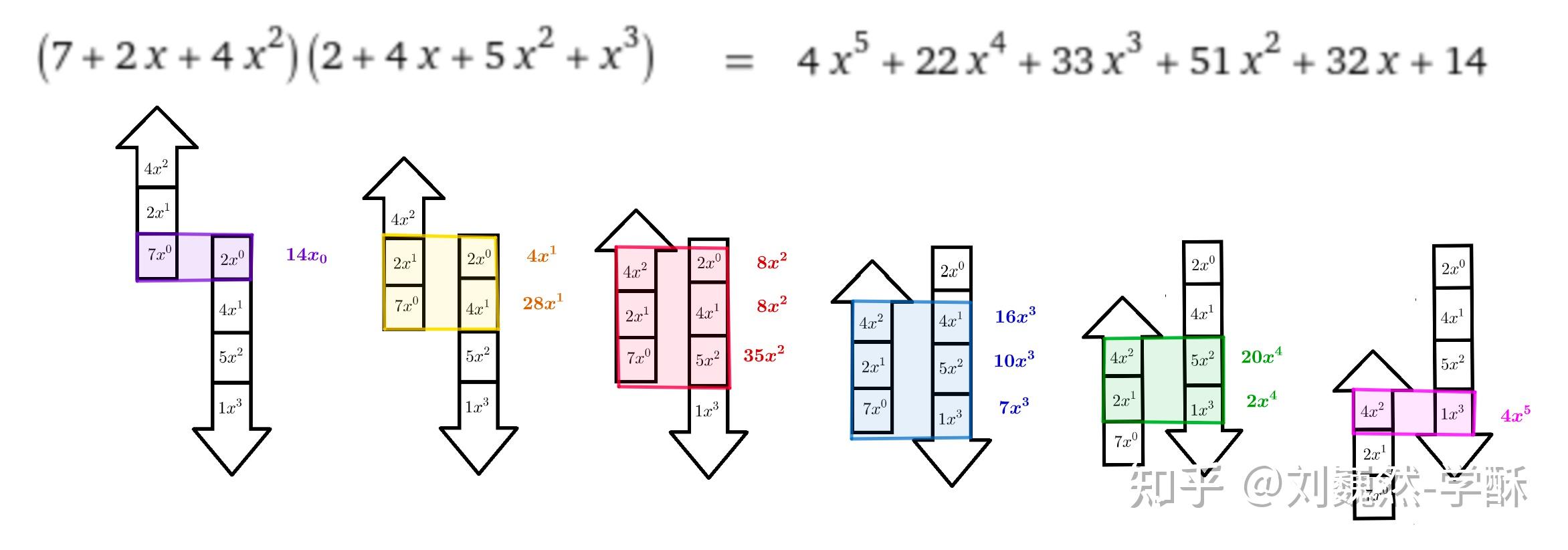
231213

conda报错

Invalid version spec: =2. 7

conda报错，原因是版本老了，可以创建一个python高版本虚拟环境。

创建虚拟环境：conda create -n [xxx] python=3.x conda=4.9.2
激活虚拟环境：conda activate [xxx]
休眠虚拟环境：conda deactivate [xxx]
虚拟环境罗列：conda info --envs 或者 conda info -e 或者 conda env list
删除虚拟环境：conda remove --name [xxx] --all
罗列虚拟环境安装的库：conda list

更换镜像源：

1
2
3

conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main/
conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/
conda config --set show_channel_urls yes

231214

宸极_231214——$GL(n,fp)$群阶的题目类型研究。

问OpenAI 3.5

一个非奇异矩阵（即可逆矩阵）的群的阶可以通过其矩阵的维度来确定。对于 n 阶矩阵，其群的阶为 $n^2 - 1$。

这是因为对于一个非奇异矩阵 A，它可以表示为 $A = PDP^(-1)$，其中 D 为对角矩阵，P 是可逆矩阵。由于 P 是可逆的，它属于 $n×n$ 可逆矩阵的集合，这个集合的阶为 $n^2$。而对角矩阵 D 的对角线上有 $n$ 个非零元素，因此 D 的阶是 $n$。所以可逆矩阵的群的阶为 $n^2 - 1$。

因此，对于一个非奇异矩阵的群的阶是 $n^2 - 1$，其中 $n$ 为矩阵的维度。

231215

安装Tesseract-OCR

单独的pytesseract包是无法运行的，需要下载Tesseract-OCR
下载链接：https://digi.bib.uni-mannheim.de/tesseract/tesseract-ocr-setup-4.00.00dev.exe
安装：按照默认的安装就行，我这里将安装路径改为D:\Programe Files\Tesseract-OCR，默认是C:\Programe Files\Tesseract-OCR
配置环境变量（这里配置的是系统变量）：
1. 新建变量：TESSDATA_PREFIX
2. 路径，Tesseract-OCR的安装路径。

231222

破解对称性的必备利器——群论

破解对称性的必备利器——群论 (qq.com)

旋转对称性

不难看出，把上面的图案 a) （顺时针或逆时针）旋转 90 度的整数倍，它都能和自己重合；图像 b) 和 k) 要（顺时针或逆时针）旋转 72 度的整数倍也能和自己重合；图像 f) 和 g) 要特殊一些，必须（顺时针或逆时针）旋转 120 度的整数倍才能和自己重合。我们把图形的这种性质称为旋转对称性（Rotational symmetry）。

此外，虽然 a) 和 e) 都具有 π/2（本文默认使用弧度制）整数倍的旋转对称性，但 e) 比 a) 更加厉害，因为如果把这两个图案沿水平或竖直方向翻折一下，e) 依然我行我素， a) 却已经迷失自我了。在这种情况下，我们称 e) 具有翻折对称性（Folding symmetry）。

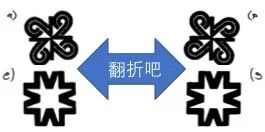
除了旋转与翻折以外，还有平移对称性，以及更加深刻的洛伦兹（时空）对称性等等。

把所有的对称性都纳入囊中呢？在数学家眼里答案只有一个字——群（Group）。

所谓一个图案的对称群，就是把所有使得它保持不变的所有动作筛选出来，凑成一个集合。不难想象，一个对称群可以由某些最基本的动作不断组合而成，这些最“基本的动作”就是对称群的生成元。

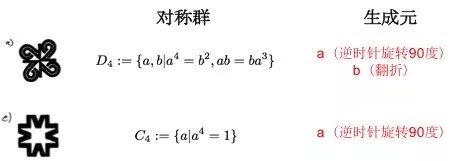
二维旋转群（二阶正交矩阵群）：

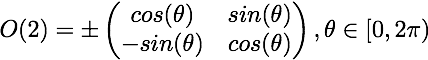
的子群。

群的定义

定义（群）：

一个群（G, ·）是由一个集合 G 和一个二元运算 · 构成的数学结构，满足：

封闭性：对于 G 中任意两个元素 a、b，a · b 也在 G 中；

结合律：对于 G 中任意两个元素 a、b、c，(a · b) · c = a · (b · c);

单位元：存在一个“单位元” e，使得对 G 中任意元素 a： e · a = a · e = a；

可逆性：G 中任意元素 a 存在一个逆元 ɐ （这个记号就是把字母 ‘a’ 倒过来），使得 a · ɐ = ɐ · a = e.

这里的二元运算 “·” 很像乘法，但不一定满足交换律。例如在旋转群例子中，先旋转再翻折和先翻折在旋转得到的效果不同！如果一个群面相良好，群“乘法”恰好满足交换律，那么这样的群称为交换群。

群的另一个例子对于有线性代数基础的读者都不陌生 —— 所有 N 阶非奇异（可逆）矩阵都能够组成一个群，而这个群的乘法就是矩阵乘法，因此这并不是交换群。数学家们把这个群称为 N 阶线性群，记作 GL(N,R) ，这里 R 表示实数全体

应用1

例如 GL(N,R) 和 GL(N,C) 是连续群，包含了一大类李群（同时具有群和流形双重属性），和与之对应的李代数（李群上的切向量场，因李群具有群的特性也同时被赋予了代数性质）关系密切。由理论物理学中著名的诺特定理（Noether‘s Theorm），每种守恒的物理量（例如质量、动量、能量等）都对应一种对称性 [1,2]，于是线性群和李群便成为了理论物理学中强有力的工具。

应用2

GL(N,Z) 和 GL(N,F_q) 都是离散群，性格和 GL(N,R) 、 GL(N,C) 两兄弟大不相同，它们被广泛地运用在数论研究中。例如 GL(N,Z) 和数论中著名的模形式（Modular Form）关系密切。简而言之，数论中的许多问题，尤其是与椭圆曲线有关的问题，可以通过研究椭圆函数（复数域上的双周期函数）来描述出来。椭圆函数属于复变函数，种类繁多，通过传统的分析方法研究并不容易；模形式是椭圆函数的一种简单表达方式，它们的对称群就是 GL(N,Z) 的一个子群（Subgroup，简要说来就是原群的一个子集合，并且这个自己和也是一个群）。

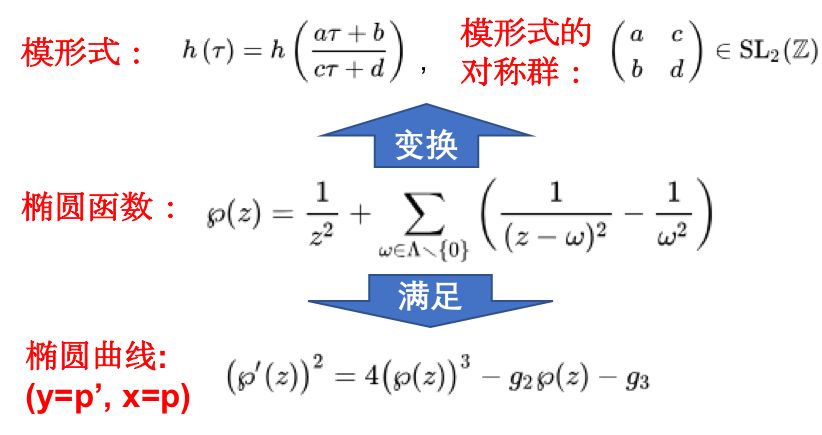
通过椭圆函数的对称群来研究椭圆函数本身，这种充满新意的想法为椭圆曲线的研究提供了全新的思路，并且同千禧年数学七大数学难题中的黎曼假设（黎曼zeta函数也是椭圆函数）和 BCS 猜想两个问题联系紧密。

群正是破解对称性的利器。

231226

确定测评目标和范围：
- 确定测评的整体目标，例如提升内容审核的准确性和高效性，确保用户发布的内容符合法规和平台规定。
- 确定测评的范围，包括审核规则、审核体系结构和使用的审核工具等。
制定测评方案：
- 规划测评的时间表和工作流程，确保测评工作能够顺利进行，并不影响平台的正常运营。
- 设计测评的方法和评估指标，用于对内容安全审核工作的实时监控、审核规则的调整、审核体系结构的设计等方面进行评估。
组织实施测评工作：
- 安排审核工作人员进行日常审核工作，并使用互联网信息审核工具进行实时监控，及时发现和处理问题。
- 收集审核工作数据和审核结果，包括审核通过率、误判率、审核的用户反馈等。
使用互联网信息审核工具实时监控审核工作，调整审核规则：
1. 部署互联网信息审核工具，对用户生成的内容进行实时监控，包括文本、图片、视频等多种形式。
2. 分析审核工作中发现的问题及用户投诉情况，以期间调整审核规则，包括敏感词库、涉黄涉暴涉政等规则的调整和优化。
3. 追踪最新的网络热点事件和舆情动态，更新审核规则以应对突发事件和舆情风险。
根据审核规则设计互联网信息审核体系结构，提出工作开发需求：
1. 根据审核规则设计审核流程和体系结构，确保审核工作的严谨性和持续性。包括责任人的职责和权限划分，审核流程的规范化和透明化。
2. 对审核工作的技术和人员需求进行评估，提出包括硬件设备、软件工具、人员培训等工作需求并提出相应的技术推荐。
根据工作汇总结果，调整内容关联拓展审核制度，调整互联网信息审核工具：
1. 对内容关联拓展的审核工作进行绩效评估，根据实际结果对关联拓展审核制度进行调整，优化审核策略，确保审核的全面性和准确性。
2. 根据最新的审核规则和审核需求，对互联网信息审核工具进行更新和调整，确保工具的适应性和灵活性。
3. 提出关于审核工具功能迭代和技术升级的工作开发需求，以适应不断变化的互联网内容特点和审核要求。

231227-8

Obsidian以及Zotero的使用。

添加文献。添加文献条目的方式有很多，个人认为以doi号添加、浏览器插件为主，以剪贴板导入为辅。

(1)首先在网上查找到文献的doi号，然后通过doi号添加条目，zotero会搜索文献信息自动添加。

通过doi号添加条目

(2)通过浏览器插件添加条目，需要借助zotero的官方浏览器插件，支持多种浏览器，可以在zotero官网直接安装，也是我添加参考文献的主要方式。安装插件后，当位于有文献信息的网页时，例如谷歌学术、知网或期刊网站等等，可以直接通过插件将当前文献保存在zotero，并且支持一次添加多篇文献。

官网提供的浏览器插件，右侧下载对应版本

使用浏览器插件添加条目

(3)通过剪贴板导入。上述两种方法基本可以应付大多文献，但对于一些特别古老的文献可能就没法识别，这是还可以通过剪贴板导入辅助添加。我们可以找到一篇文献的参考文献信息(或者自己手动整理)，然后复制到剪贴板，然后在zotero中选”文件”->”从剪贴板导入”或者按快捷键”Ctrl+Shift+Alt+I”来导入文献。

从剪贴板导入条目

一般导入文献之后，并不能保证文献信息一定是正确的，还需要养成主动检查的习惯。

-------------THE END-------------