Weekly-Descriptions-About-Crypto

Posted on Edited on In Symbols count in article: 6k Reading time ≈ 5 mins.

The dp_leakage in RSA attacks, the post will introduce some extensions about the dp_leakage, using the example [2020YCB]Power.

Next part will resolve the [2022MIMIC]cry1 which is more easier than the former wp. The former by using polynomial, the latter by using math deduction with fermat_little_theorem.

Both of them will be given full solutions and comparison.

DP_LEAKAGE_EXTENSIONS

EX1: $n = p^{b}\cdot q$

[2020YCB]Power

1
2
3
4
5
6
7
8
9
10
11
12
def dp_hensel(c, e, dp, p, b):
    """
    :param b: p^b*q
    :return: m
    """
    mp_ = pow(c, dp, p)
    mp = pow(c, dp - 1, p)
    for i in range(1, b - 2):
        x = pow(c - pow(mp_, e), 1, p**(i + 1))
        y = pow(x * mp * invert(e, p), 1, p**(i + 1))
        mp_ = mp_ + y
    return mp_

EX2: Coppersmith attack, know dp high

[qwb2019]Coppersmith

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#Sage
dp0 = 
e = 
n = 

F.<x> = PolynomialRing(Zmod(n))
d = inverse_mod(e, n)
for k in range(1, e):
	f = (secret << 200) + x + (k - 1) * d # 200 editable
	x0 = f.small_roots(X=2 ** (200 + 1), beta=0.44, epsilon=1/32)
	if len(x0) != 0:
		dp = x0[0] + (secret << 200)
		for i in range(2, e):
			p = (e * Integer(dp) - 1 + i) // i
			if n % p == 0:
				break
		if p < 0:
			continue
		else:
			print('k = ',k)
			print('p = ',p)
			print('dp = ',dp)
			break

EX3: $p = gcd(m^{e\cdot dp} - m, n)$

TBC

[2020YCB]Power

Power.py

factorize $n$ to get $p$

solution1-limit

Use the bit_length of $p$ to limit. We can get the equation of $num = dp \times e - 1$, and the num’s bit_length is 526, meaning that num contains some excess factors. We divide these small factors and we will get the true $p$, whose bit_length is 512.

We use yafu to make a factorization.

Deduction:
$$
\varphi(n) = lcm(p-1, q-1) = k_1(p-1) \cdot k_2(q-1)
$$

$$
d \times e \equiv 1 \mod \varphi(n) \equiv 1 \mod (p-1)
$$

$$
dp \equiv d \mod (p-1)
$$

$$
\Longrightarrow dp\times e \equiv 1 \mod (p-1)
$$

Meaning that $num = dp \times e - 1 = k(p-1)$, we limit the bit_length to 512, and we will get the key equation of $p = num + 1$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
"""
factor:
P1 = 2 # 1 digits
P1 = 2
P1 = 2
P2 = 11 # 2
P4 = 7411 # 4
P14 = 10402958442703 # 14
P17 = 25388174482857437 # 17
P23 = 19976951634728916570101 # 23
P33 = 121098273308863403811867260913043 # 33
P69 = 514664028984426592785192432611128951474323755859087258008037664208623 # 69
"""
p = num // 7411 // 2 // 2 + 1
# judgement conditions
# 1. the bit_length 512 ?
# 2. p is prime ?

solution2-root

Use the equation of $x = 2019\times p^{2} + 2020\times p^{3} + 2021\times p^{4}$ , which is given by Power.py . We can also see clearly from the Power.py that it use discrete log to generate $g_1$, by using $x, y, g$.

So the steps to solve $p$:

  • discrete_log(y, c1, g) to solve out $x$ (more important)
  • equations to solve out $p$, the root of the equation is $p$

The real $p$ is defined in $GF(y)$

1
2
3
4
5
6
7
8
9
10
# step1
x = discrete_log(y, c1, g)
# x =

# step2
p = var('p')
R.<p> = PolynomialRing(GF(y))
f = 2019*p**2 + 2020*p**3 + 2021*p**4 - x
f.roots()
# p =

solution3-crack

Just crack by using the $dp, e, x, y, c1$. 

1
2
3
4
5
6
7
for x in range(1,e+1):
    if (dp*e-1)%x==0:
        p=(dp*e-1)//x+1
        x = 2019*p**2 + 2020*p**3 + 2021*p**4
        if c1 == pow(g, x, y):
            print(p)
            break

solve out $m$

solution1-deduce

Use fermat_little_theorem to deduce. From the definition of $c$.
$$
c \equiv m^{e} \mod n
$$

$$
dp \equiv d \mod (p-1)
$$

$$
\rightarrow c^{dp} \equiv m^{dp \cdot e}\mod n
$$

$$
\Longrightarrow \exists k \in \mathbb{Z}, c^{dp}\mod p = m^{k\cdot (p-1) + 1} \mod p
$$

Fermat's little theorem can get the equation of $m^{\varphi(p)}\mod p \equiv 1$.
$$
\Longrightarrow m \cdot m^{k\cdot(p-1)}\mod p \equiv c^{dp} \mod p
$$

$$
\Longrightarrow m \equiv c^{dp} \mod p
$$

So we can run this easy code to get $m$.

1
m = pow(c, dp, p)

solution2-hensel

The $n = p^{4}\times q$, which is satisfied the hensel_lifting scheme. The $b$ is 4. 

1
m = int(dp_hensel(c, e, dp, p, b))

Over~

[2022MIMIC]cry1

cry1.py

references:

  • V&N2020 Fast
  • REDHAT2019 Related

part1

To solve out the $p$ and $q$, we ought to make a deduction about the encrypt code.

Known:
$$
g_1 = g^{(p-1) \cdot r_1}\mod p
$$

$$
c_1 \equiv (m \times g_1^{s_1} \mod N )\mod N
$$

Deduction: fermat_little_theorem
$$
g_1 = g^{(p-1)\cdot r1} \mod p \equiv 1
$$

$$
\Longrightarrow g_1 - 1 = k\cdot p
$$

The $N = p\times q$, thus we can get $p$ by $gcd(g_1-1, N)$. 

1
2
p = gcd(g1 - 1, N)
q = N // p

solution1-crt

Write the decrypt code by using chinese_remainder_theorem. 

1
2
3
4
5
6
7
8
def decrypt(c1, c2, p, q):
    xp = c1 % p
    xq = c2 % q
    # Chinese Remainder Theorem
    m = (xp*invert(q, p)*q + xq*invert(p, q)*p) % (p*q)
    return m
# or sagemath-crt()
m = crt([c1, c2], [p, q])

solution2-min

$$
c_1 \equiv (m \times g^{s_1 \cdot r_1 \cdot (p-1)} \mod p) \mod N\
\Longrightarrow c_1 \equiv m \mod N
$$

By equation above, we can get a simple way to solve out $m$, for that the bit_length of $m$ is short theoretically.
$$
m = min(c1 \mod p, c1 \mod q)
$$
Convert to code.

1
m = min(c1 % p, c1 % q)

part2

Three equations of A, B, C. 

1
2
3
4
cnt = len(Cs)
A = [(i + 128)**2 for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
C = [(i + 512) for i in range(cnt)]

solution1-Groebner_basis

1
2
3
4
5
6
7
8
9
10
11
12
PR = PolynomialRing(Zmod(N2), 'x', cnt)
x = PR.gens()
Fs = [((A[i] * x[i]**2 + B[i] * x[i] + C[i])**e - Cs[i]) for i in range(cnt)]
Fs.append(x[0] + x[1] + x[2] - S)
I = Ideal(Fs)
G_b = I.groebner_basis()
m2 = ''
for b in G_b[:-1]:
    mi = ZZ(-b(0, 0, 0))
    mi = hex(mi)[2:].strip('L')
    m2 += (('', '0')[len(mi) %2]+mi)
# m is hex

TBC~

solution2-functions

We are similar to the polynomial equations, thus we make a conversion.

Get the quadradic equations by open to the power of e.

1
2
3
C_ = []
for i in Cs:
    C_.append(iroot(i, Cs)[0])

Unknown variables $m1, m2, m3$defined on the ring of $\mathbb{Z}$ .

1
2
3
P.<m1> = Zmod()[]
P.<m2> = Zmod()[]
P.<m3> = Zmod()[]

Substitute the former equations, and get the quadradic equations. 

1
2
3
f1 = A[0] * m1 ** 2 + B[0] * m1 + C[0] - int(C_[0])
f2 = A[1] * m2 ** 2 + B[1] * m2 + C[1] - int(C_[1])
f3 = A[2] * m3 ** 2 + B[2] * m3 + C[2] - int(C_[2])

Get the root. 

1
2
3
v1 = f1.roots()
v2 = f2.roots()
v3 = f3.roots()

coppersmith边界问题

RSA中coppersmith定理的应用条件_small_roots_M3ng@L的博客-CSDN博客

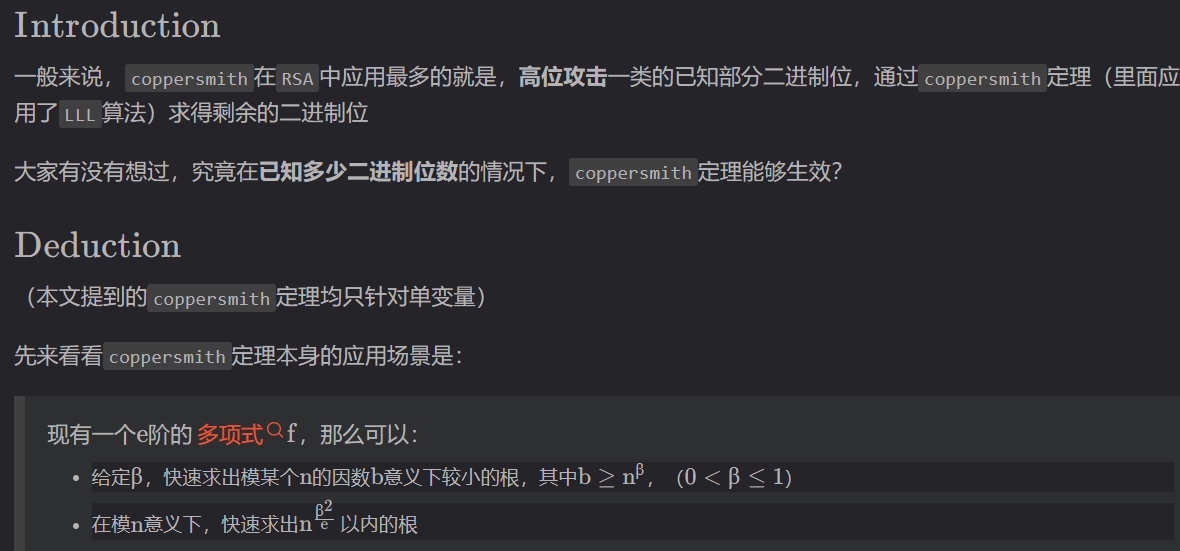
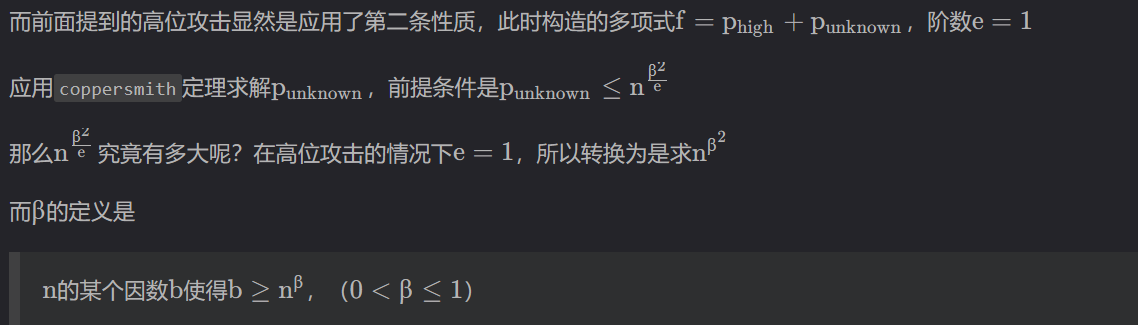
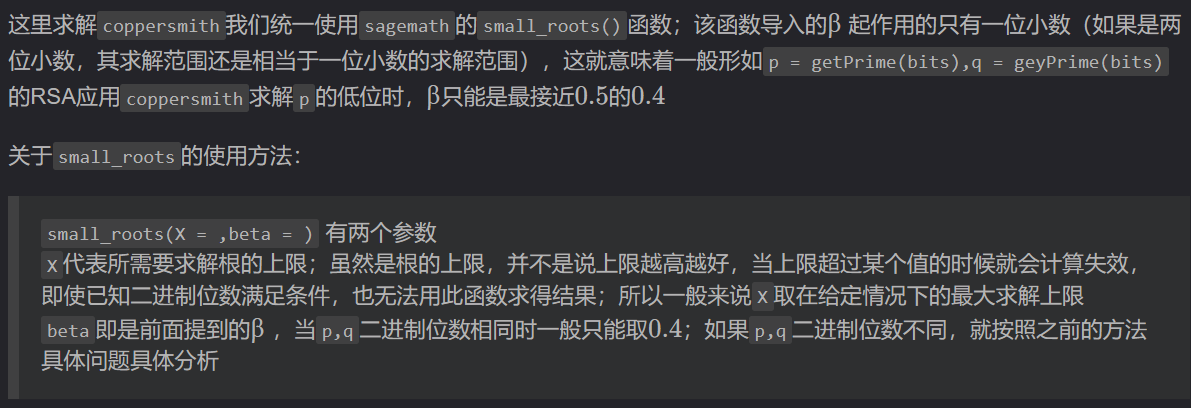
  • 在sagemath中应用coppersmith定理的函数有两个：small_roots， coppersmith_howgrave_univariate。

  • 这里求解coppersmith我们统一使用sagemath的small_roots()函数；该函数导入的 $\beta$起作用的只有一位小数（如果是两位小数，其求解范围还是相当于一位小数的求解范围），这就意味着一般形如p = getPrime(bits),q = geyPrime(bits)的RSA应用coppersmith求解$p$的低位时，$\beta$只能是最接近$0.5$ 的$0.4$。

关于small_roots()的使用方法：

1
small_roots(X = ,beta = ) 有两个参数

$X$代表所需要求解根的上限；虽然是根的上限，并不是说上限越高越好，当上限超过某个值的时候就会计算失效，即使已知二进制位数满足条件，也无法用此函数求得结果；所以一般来说$X$取在给定情况下的最大求解上限。

$beta$即是前面提到的$\beta$ ，当$p$,$q$二进制位数相同时一般只能取$0.4$；如果$p$,$q$二进制位数不同，就按照之前的方法具体问题具体分析。

经过测试得到，当未知量小于等于$454bits$时（$p$,$q$为$1024bits$），coppersmith定理可以求解

之后改变了$p$,$q$的大小，经过测试发现，当$p$,$q$同二进制位数时，要使用small_roots()应用coppersmith定理求解$n$的某个因数的低位，需要满足未知的二进制位数与因数之间的二进制位数的关系是：
$$
bits_{unknown} \div bits_{p} < = 0.44
$$

-------------THE END-------------