23-01-11-ECC

Some basics about elliptic curves. Make a description about ECC, and show the attacks and conversions to code.

ECC is somewhat difficult, and also the analysis which is necessary ought to be detailed.

The ECC always connects to the usage of sagemath, this post also introduces some common usages about ECC in sagemath.

PARALLEL

Assume: Parallel lines intersect at infinity which is called the infinity point P. (parallel and intersecting unity)

The properties of infinite P:

• The infinite P of Line L has only one.
• The lines which are parallel to each other have the public infinite $P_{\infty}$.
• Any lines which are intersect have different infinite points $P_{\infty}$s. (If they have public infinity, it will contrary to assumption.)
• All infinity points formulate a infinity line.
• The total infinity points and all ordinary points in the plane form the projective plane.

PROJECTIVE PLANE COORDINATE SYSTEM

Formulate: Make $x = X/Z$, $y = Y/Z$, ($Z \neq 0$), and the Point A is $(X:Y:Z)$.

The infinity points are expressed as $(X:Y:0)$. The ordinary points is $Z \neq 0$,and the infinities are $Z = 0$, meaning that the equation of infinity points is $Z = 0$.

Thus, $(X:Y:Z)$ is called as projective plane coordinate system.

ELLIPTIC CURVE

Definition: The elliptic curve in projective plane satisfies the equation that $Y^2Z + a_1XYZ + a_3YZ^2 = X^3 + a_2X^2Z + a_4XZ^2 + a_6Z^3$, or Weierstrass homogeneous equation $Y^2=X^3+AX+B$, where the whole points are non-singular or smooth.

Non-singular/Smooth: Mathematically, the partial derivatives $F_x(x,y,z), F_y(x,y,z),F_z(x,y,z)$ at any point on the curve cannot be 0 at same time, meaning that any point exists tangent.

Assume that $x = X/Z, y= Y/Z$ and substitute into the equation above, we can obtain $y^2 + a_1xy + a_3y = x^3 + a_2x^2+a_4x+a_6$ and also the slope is $k = (3x^2+2a_2x+a_4 - a_1y)/(2y + a_1x+a_3)$.

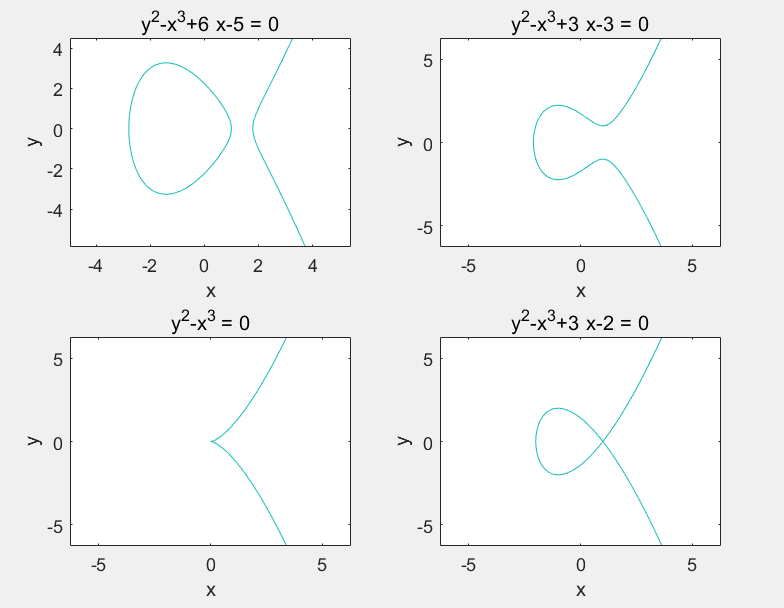
Two curves below which are not satisfied the definition are not elliptic curves , and they are called Singular Curves.

ALGORITHM ON AN ELLIPTIC CURVE

Algorithm: Arbitrarily take two points P and Q on the elliptic curve (if the two points P and Q coincide, then make the tangent of point P), make the line intersect the other point R' of the elliptic curve, and cross R' to make the parallel line of the y axis intersect the point R, we specify $P+Q = R$.

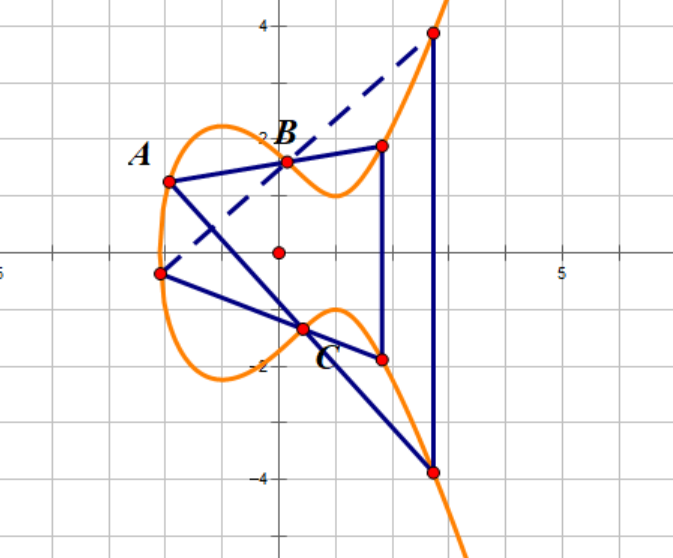
The infinity $O_{\infty}$ and the point $P$ on the elliptic curve intersect at the point $P$. The action of of infinity $O_{\infty}$ is equivalent to 0, which is called the zero element. The equation is that $O_{\infty} + P = P$.

Deduction:

• Three points on elliptic curve are in the straight line $A + B + C = O_{\infty}$.
• The sum of $k$ identical points is denoted $kP$. eg: $P+P+P = 2P+P = 3P$

Notice: Elliptic curves are not necessarily symmetric with respect to x-axis.

ELLIPTIC CURVE IN CRYPTOGRAPHY

Discretization: Define elliptic curves on finite field.

Algorithm:

• Finite field $F_p$ only has finite elements.

• $F_p$ has $p$ elements. $F_p \in {0, 1, 2, 3, \dots, p-1}$

• +:$a + b \equiv c \mod p$

• ×:$a \times b \equiv c \mod p$

• ÷:$a \times b^{-1} \equiv c \mod p$

• Unit element = 1 ; Zero element = 0

The elliptic curves that are suitable for encryption: $y^2 = x^3 + ax + b$.

The relationship among $P(x_1, y_1), Q(x_2, y_2)$ and $R(x_3, y_3)$:

• $x_3 \equiv k - x_1 - x_2 (\mod p)$
• $y_3 \equiv k(x_1 - x_3) - y1(\mod p)$
• $k$
  • if $P = Q$, the $k = (3x^2 + a)/2y_1$
  • if $P \neq Q$, the $k = (y_2 - y_1)/(x_2 - x_1)$

Point P exists the minimum positive integer $n$, which make $np = O_{\infty}$, and we will call $n$ as the order of n. Otherwise, it is called infinite order.

n always exists.

SIMPLE ENCRYPTION AND DECRYPTION ON ELLIPTIC CURVES

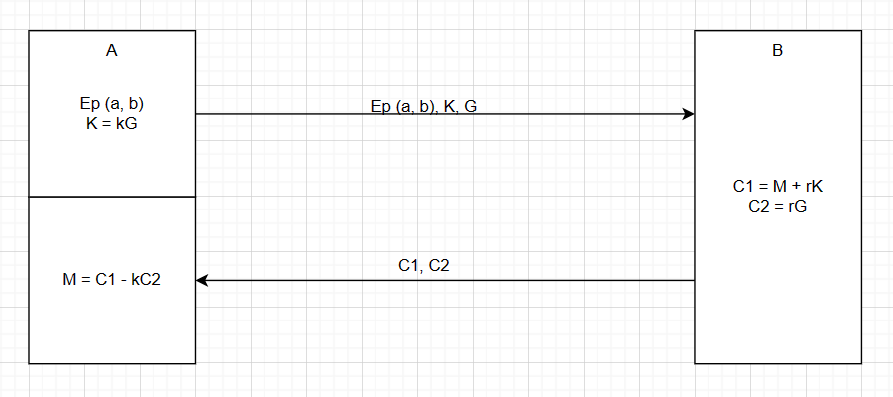
• A as the generator and decryptor. B as the encryptor.

• A generates the basic parameters. The $(a, b)$ is to generate the elliptic curve. The $G$ is the chosen base point. Then, send $E_p(a, b), K, G$ to B.

• B generates the random $r$. Make a encryption and send $C_1 = M + rK,C_2 = rG$ to A.

• A decrypts the ciphers by the equation $M = C1 - kG_2$. Finally, A will get message $M$.

• PubKey: $K = kG$

• PriKey: $k$

Common 6 parameters $F(p,a,b,G,n,h)$:

• $p, a, b \rightarrow E_p(a, b)$: $p$ 200 more digits can ensure the security.
• $G$: the chosen base point of $E_p(a, b)$
• $n$: the order of $E_p(a, b)$
• $h$: the cofactor and the integer part that $m$, the sum of all points on elliptic curve, divides $n$.

ATTACKs

The important part.

Make some description about the common attacks on elliptic curves in cryptography.

Pohlig-Hellman

The order of elliptic curve is factorized into small primes.

Main idea:

1. Factorize the order.
2. Discrete logarithmic problems in factorized primes.
3. Chinese reminder theorem.

Deduction:

Example: ECC-2

# polig_hellman
a2 = 377999945830334462584412960368612
b2 = 604811648267717218711247799143415167229480
p2 = 1256438680873352167711863680253958927079458741172412327087203
E2 = EllipticCurve(GF(p2), [a2, b2])
P2 = E2(550637390822762334900354060650869238926454800955557622817950 ,700751312208881169841494663466728684704743091638451132521079 )
Q2 = E2(1152079922659509908913443110457333432642379532625238229329830 , 819973744403969324837069647827669815566569448190043645544592 )

factors, exponents = zip(*factor(P2.order()))
# print(factors)
# print(exponents)
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-1]
# print(primes)
dlogs = []
for fac in primes:
    t = int(P2.order()) // int(fac)
    dlog = discrete_log(t*Q2, t*P2, operation = '+')
    dlogs += [dlog]
# print(dlogs)
if len(primes) == len(dlogs):
    m2 = crt(dlogs, primes)
flag2 = long_to_bytes(m2).decode()
print(flag2)

Smart Attack

$E(F_p) = p$, the order of the elliptic curve is a prime.

It will be updated, if I have time.

Exp: ECC-3

# smart_attack
a3 = 490963434153515882934487973185142842357175523008183292296815140698999054658777820556076794490414610737654365807063916602037816955706321036900113929329671
b3 = 7668542654793784988436499086739239442915170287346121645884096222948338279165302213440060079141960679678526016348025029558335977042712382611197995002316466
p3 = 11093300438765357787693823122068501933326829181518693650897090781749379503427651954028543076247583697669597230934286751428880673539155279232304301123931419
E3 = EllipticCurve(GF(p3), [a3, b3])
P3 = E3(10121571443191913072732572831490534620810835306892634555532657696255506898960536955568544782337611042739846570602400973952350443413585203452769205144937861 , 8425218582467077730409837945083571362745388328043930511865174847436798990397124804357982565055918658197831123970115905304092351218676660067914209199149610 )
Q3 = E3(964864009142237137341389653756165935542611153576641370639729304570649749004810980672415306977194223081235401355646820597987366171212332294914445469010927 , 5162185780511783278449342529269970453734248460302908455520831950343371147566682530583160574217543701164101226640565768860451999819324219344705421407572537 )

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

# from gmpy2 import is_prime
# print(is_prime(P3.order()))
m3 = SmartAttack(P3, Q3, p3)
flag3 = long_to_bytes(m3).decode() + '}'
print(flag3)

BSGS

baby step giant step

discrete_log(P,Q,operation = ‘+’)

Problems: $y^x \equiv z \mod p$

To solve out the $x$.

Original

$gcd(y, p) = 1$

Assume $x = am - b,m = \sqrt{p}$, $a \in [0, m), b\in[0, m)$.

Derivation:
$$
y^{am-b}\equiv z (\mod p)
$$

$$
y^{am} \equiv z \cdot y^{b}(\mod p)
$$

Brute force enumeration, enumerate the right in $[0, m)$ and calculate into list. At the same time, we enumerate the left in $[0, m)$, comparing the two list to find the $x$.

Extended

$gcd(y, p) \neq 1$

Assume $d = gcd(y, p)$.

Derivation:
$$
y^{x} + kp =z
$$

$$
y\cdot y^{x-1} +kp = z
$$

If we divide it by $d$., we will get that:
$$
\frac{y}{d}\cdot y^{x-1} + k \cdot \frac{p}{d} =\frac{z}{d}
$$
Recursive the equation, unless $d = 1 $. Assume that the product of all $d$ and we enumerate $c$ times. Thus, we can obtain the condition that $x’ = x -c, p’ = \frac{p}{g}, z’ = \frac{z}{g}$.
$$
y^{x’} \cdot \frac{y^{c}}{g} \equiv z’ (\mod p’)
$$
And it convert to the original BSGS.

Example: ECC-1

# bsgs
a1 = 46056180
b1 = 2316783294673
p1 = 146808027458411567
E1 = EllipticCurve(GF(p1), [a1, b1])
P1 = E1(119851377153561800 , 50725039619018388)
Q1 = E1(22306318711744209 , 111808951703508717)
m1 = discrete_log(Q1, P1, operation = '+')
flag1 = 'flag{' + long_to_bytes(m1).decode()
# print(flag1)

ECC

Definition

The equation:
$$
(a, b)\in F, y^2 = x^3 + ax + b
$$
$$
\Delta = 4a^{3} + 27b^{2} \ne 0
$$

if the ECC satisfies the equation, we calculate its discriminant by:
$$
y^2 + axy + by = x^3 + cx^2 + dx + c
$$

Test

https://lbwang.github.io/2020/04/08/ecc/

a = -5; b = 4
E1 = EllipticCurve(RR, [a, b])
show(plot(E1, hue=.9))

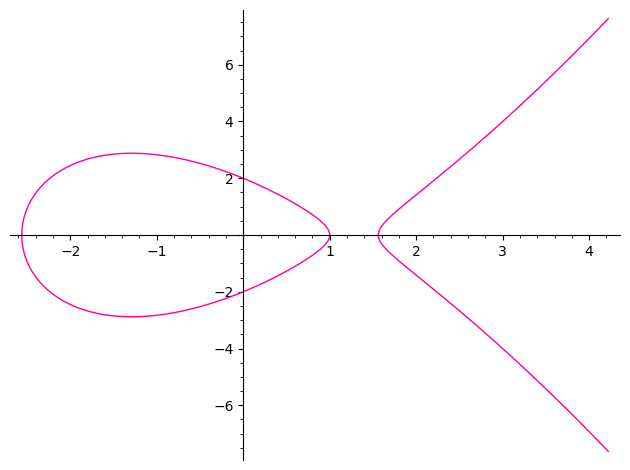
if we change the figure of $a$ and $b$, we can get the other EllipticCurves.

a = 2; b = 3
E2 = EllipticCurve(RR, [a, b])
show(plot(E2, hue=.9))

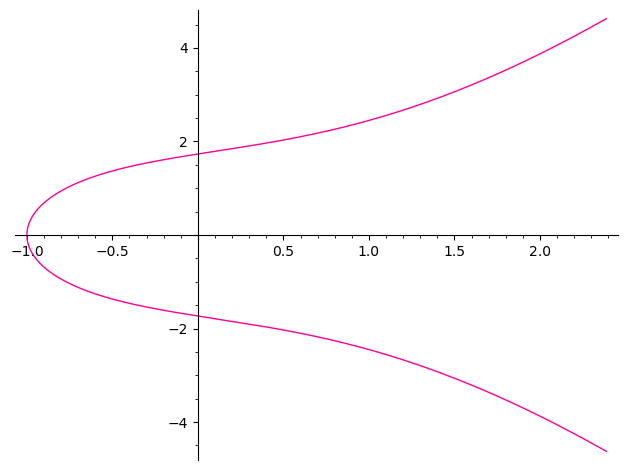
or we make the $a$ and $b$ random, thus we can not predict the curves.

E3 = EllipticCurve(RR, [RR.random_element(), RR.random_element()])
show(plot(EE, hue=.7))

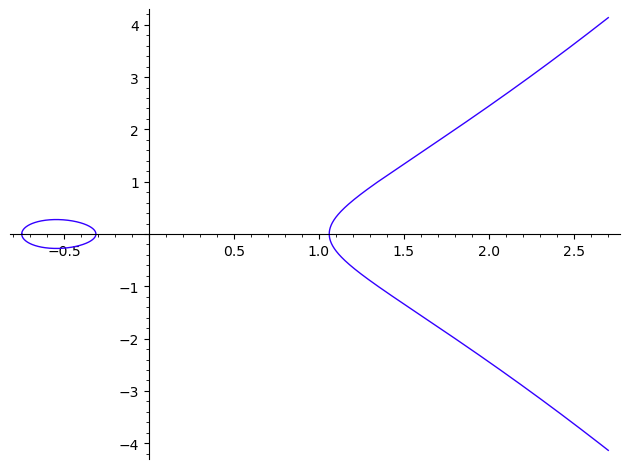
sage: p = 137
sage: F = GF(p)
sage: F = FiniteField(p)
sage: F = GF(p)
sage: E137 = EllipticCurve(F, [F.random_element(), F.random_element()])
sage: show(plot(E137, hue=.7))
Launched png viewer for Graphics object consisting of 1 graphics primitive
sage: